题目内容
(本小题满分12分)
在平面直角坐标系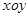 中,点
中,点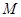 到两定点F1
到两定点F1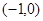 和F2
和F2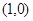 的距离之和为
的距离之和为 ,设点
,设点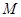 的轨迹是曲线
的轨迹是曲线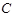 .(1)求曲线
.(1)求曲线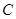 的方程; (2)若直线
的方程; (2)若直线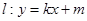 与曲线
与曲线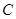 相交于不同两点
相交于不同两点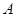 、
、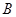 (
(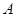 、
、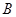 不是曲线
不是曲线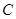 和坐标轴的交点),以
和坐标轴的交点),以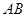 为直径的圆过点
为直径的圆过点 ,试判断直线
,试判断直线 是否经过一定点,若是,求出定点坐标;若不是,说明理由.
是否经过一定点,若是,求出定点坐标;若不是,说明理由.
(1) 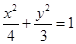 ;(2)直线
;(2)直线 过定点,定点坐标为
过定点,定点坐标为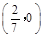 .
.
解析试题分析:(1)设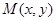 ,由椭圆定义可知,
,由椭圆定义可知,
点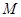 的轨迹
的轨迹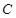 是以
是以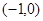 和
和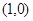 为焦点,长半轴长为2的椭圆.
为焦点,长半轴长为2的椭圆.
它的短半轴长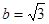 ,故曲线
,故曲线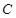 的方程为:
的方程为: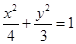
(2)设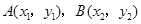 .
.
联立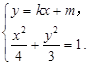 消去y,整理得
消去y,整理得 ,
,
则 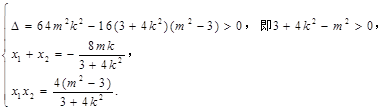
又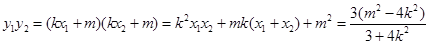 .
.
因为以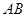 为直径的圆过点
为直径的圆过点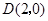 ,
,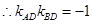 ,即
,即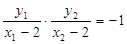 .
.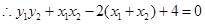 .
.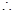
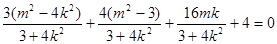 .
.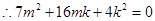 .
.
解得: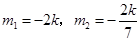 ,且均满足
,且均满足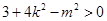 .
.
当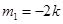 时,
时, 的方程
的方程 ,直线过点
,直线过点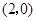 ,与已知矛盾;
,与已知矛盾;
当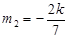 时,
时, 的方程为
的方程为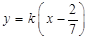 ,直线过定点
,直线过定点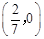 .
.
所以,直线 过定点,定点坐标为
过定点,定点坐标为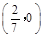 .
.
考点:本题主要考查椭圆的定义及标准方程,直线与椭圆的位置关系。
点评:典型题,关于椭圆的考查,往往以这种“连环题”的形式出现,首先求标准方程,往往不难。而涉及在直线与椭圆的位置关系,往往要利用韦达定理,实现“整体代换”。

练习册系列答案
相关题目
 的中心在原点,焦点在
的中心在原点,焦点在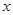 轴上,一条经过点
轴上,一条经过点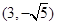 且方向向量为
且方向向量为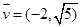 的直线
的直线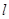 交椭圆
交椭圆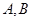 两点,交
两点,交 点,且
点,且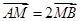 .
.
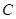 的圆心为原点
的圆心为原点 ,且与直线
,且与直线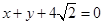 相切。
相切。
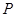 在直线
在直线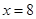 上,过
上,过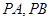 ,切点为
,切点为 ,求证:直线
,求证:直线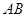 恒过定点。
恒过定点。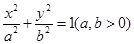 的焦点坐标为
的焦点坐标为 (
( ),点M(
),点M(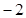 ,
,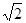 )在椭圆E上.
)在椭圆E上.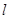 与椭圆E交于
与椭圆E交于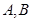 两点,求线段
两点,求线段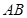 中点
中点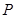 的轨迹方程;
的轨迹方程;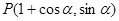 ,参数
,参数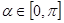 ,点Q在曲线C:
,点Q在曲线C: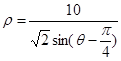 上.
上. 的轨迹方程和曲线C的方程;
的轨迹方程和曲线C的方程; 中,椭圆
中,椭圆 的焦距为2,且过点
的焦距为2,且过点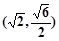 .
.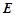 的方程;
的方程;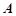 ,
, 分别是椭圆
分别是椭圆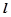 经过点
经过点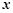 轴,点
轴,点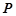 是椭圆上异于
是椭圆上异于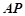 交
交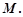
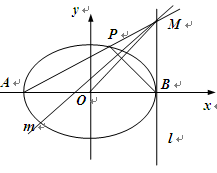
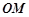 的斜率为
的斜率为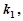 直线
直线 的斜率为
的斜率为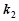 ,求证:
,求证: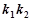 为定值;
为定值; 垂直于
垂直于 的直线为
的直线为 .求证:直线
.求证:直线 ,椭圆
,椭圆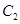 以
以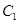 的长轴为短轴,且与
的长轴为短轴,且与 ,求直线
,求直线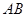 的方程.
的方程.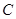 的顶点为坐标原点
的顶点为坐标原点 ,焦点
,焦点 在
在 轴上,准线
轴上,准线 与圆
与圆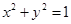 相切.
相切.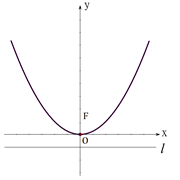
 在抛物线
在抛物线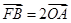 ,求点
,求点 的坐标.
的坐标.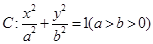 的焦点为
的焦点为 、
、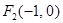 ,离心率为
,离心率为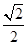 ,过点
,过点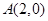 的直线
的直线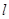 交椭圆
交椭圆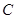 于
于 、
、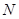 两点.
两点.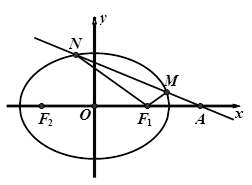
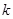 的取值范围;
的取值范围;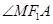 和
和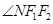 是否总相等?若相等,请给出证明,若不相等,说明理由.
是否总相等?若相等,请给出证明,若不相等,说明理由.