题目内容
(本小题满分10分)
已知点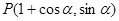 ,参数
,参数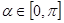 ,点Q在曲线C:
,点Q在曲线C: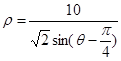 上.
上.
(1)求在直角坐标系中点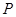 的轨迹方程和曲线C的方程;
的轨迹方程和曲线C的方程;
(2)求|PQ|的最小值.
(1)点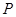 的轨迹是上半圆:
的轨迹是上半圆: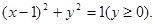 曲线C的直角坐标方程:
曲线C的直角坐标方程: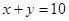 (2)
(2)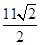 -1
-1
解析试题分析:设点P的坐标为(x,y),则有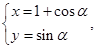 消去参数α,可得
消去参数α,可得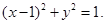 由于α∈[0,π],∴y≥0,故点P的轨迹是上半圆
由于α∈[0,π],∴y≥0,故点P的轨迹是上半圆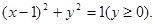 ∵曲线C:
∵曲线C: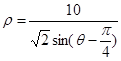 ,即
,即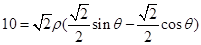 ,即 ρsinθ-ρcosθ=10,故曲线C的直角坐标方程:x-y+10=0.(2)如图所示:由题意可得点Q在直线x-y+10="0" 上,点P在半圆上,半圆的圆心C(1,0)到直线x-y+10=0的距离等于
,即 ρsinθ-ρcosθ=10,故曲线C的直角坐标方程:x-y+10=0.(2)如图所示:由题意可得点Q在直线x-y+10="0" 上,点P在半圆上,半圆的圆心C(1,0)到直线x-y+10=0的距离等于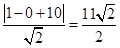 .即|PQ|的最小值为
.即|PQ|的最小值为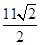 -1.
-1.
考点:本题考查了把参数方程、极坐标方程化为直角坐标方程的方法及直线与圆的位置关系
点评:对于参数方程与极坐标的考查,主要的就是考查参数方程和极坐标转化为普通方程的过程,有时需要注意参数和极坐标的角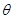 的范围.直线的极坐标方程的建立一般是通过直角三角形来处理
的范围.直线的极坐标方程的建立一般是通过直角三角形来处理

练习册系列答案
相关题目
 的方程为
的方程为 它的离心率为
它的离心率为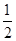 ,一个焦点是(-1,0),过直线
,一个焦点是(-1,0),过直线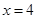 上一点引椭圆
上一点引椭圆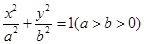 上的点
上的点 处的切线方程是
处的切线方程是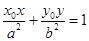 .求证:直线AB恒过定点C,并求出定点C的坐标;
.求证:直线AB恒过定点C,并求出定点C的坐标;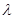 ,使得求证:
,使得求证: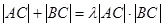 (点C为直线AB恒过的定点).若存在
(点C为直线AB恒过的定点).若存在 (
(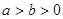 ),点
),点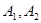 为椭圆C的左、右顶点。
为椭圆C的左、右顶点。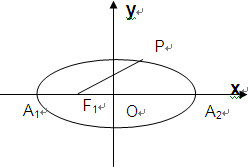
 与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足
与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足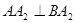 ,求证:直线
,求证:直线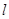 过定点,并求出该点的坐标。
过定点,并求出该点的坐标。 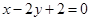 经过椭圆
经过椭圆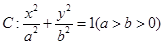 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆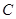 的右顶点为
的右顶点为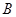 ,点
,点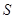 和椭圆
和椭圆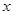 轴上方的动点,直线,
轴上方的动点,直线,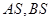 与直线
与直线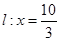 分别交于
分别交于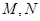 两点。
两点。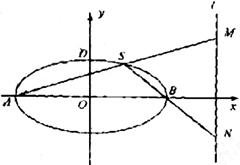
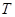 ,使得
,使得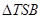 的面积为
的面积为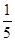 ?若存在,确定点
?若存在,确定点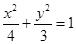 ,抛物线C2:
,抛物线C2: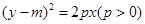 ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.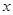 轴时,求
轴时,求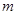 、
、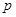 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;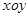 中,点
中,点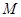 到两定点F1
到两定点F1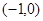 和F2
和F2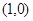 的距离之和为
的距离之和为 ,设点
,设点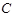 .(1)求曲线
.(1)求曲线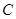 的方程; (2)若直线
的方程; (2)若直线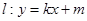 与曲线
与曲线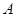 、
、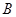 (
(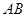 为直径的圆过点
为直径的圆过点 ,试判断直线
,试判断直线 是否经过一定点,若是,求出定点坐标;若不是,说明理由.
是否经过一定点,若是,求出定点坐标;若不是,说明理由.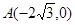 是其左顶点,点C在椭圆上且
是其左顶点,点C在椭圆上且 ·
· ="0," |
="0," |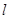 和椭圆交于M,N两个不同点,求
和椭圆交于M,N两个不同点,求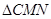 面积的最大值,并求此时直线
面积的最大值,并求此时直线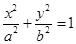 (a,b>0)过M(2,
(a,b>0)过M(2,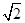 ) ,N(
) ,N(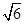 ,1)两点,O为坐标原点.
,1)两点,O为坐标原点.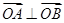 ?若存在,写出该圆的方程,若不存在说明理由。
?若存在,写出该圆的方程,若不存在说明理由。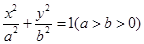 的离心率为
的离心率为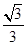 ,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.
,直线l: y-=x+2与.以原点为圆心、椭圆C1的短半轴长为半径的圆O相切.