题目内容
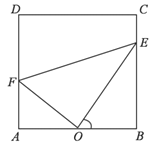
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
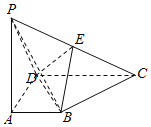
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面
平面![]() ;
;
![]() Ⅱ
Ⅱ![]() 若二面角
若二面角![]() 大于
大于![]() ,求四棱锥
,求四棱锥![]() 体积的取值范围.
体积的取值范围.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
![]() Ⅰ
Ⅰ![]() 先推导出
先推导出![]() ,从而
,从而![]() 平面
平面![]() ,可得
,可得![]() ,结合
,结合![]() ,利用线面垂直的判定定理能证明
,利用线面垂直的判定定理能证明![]() 平面
平面![]() ;
;![]() Ⅱ
Ⅱ![]() 以
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,分别求出平面
,分别求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,由二面角
的法向量,由二面角![]() 大于
大于![]() ,可得
,可得![]() ,进而能求出四棱锥
,进而能求出四棱锥![]() 体积的取值范围.
体积的取值范围.
![]() Ⅰ
Ⅰ![]() 平面
平面![]() 平面ABCD,
平面ABCD,![]() ,E是棱PC的中点,
,E是棱PC的中点,
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() 平面PAD,
平面PAD,
![]() ,
,![]() ,
,
![]() 平面ABCD.
平面ABCD.
![]() Ⅱ
Ⅱ![]() 以A为原点,AB为x轴,AD为y轴,AP为z轴,
以A为原点,AB为x轴,AD为y轴,AP为z轴,
建立空间直角坐标系,
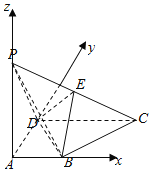
设![]() ,则
,则![]() 0,
0,![]() ,
,![]() 2,
2,![]() ,
,![]() 0,
0,![]() ,
,
![]() 2,
2,![]() ,
,![]() 1,
1,![]() ,
,
![]() 2,
2,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,
设平面BDP的法向量![]() y,
y,![]() ,
,
则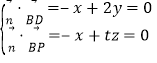 ,取
,取![]() ,得
,得![]() 1,
1,![]() ,
,
设平面BDE的法向量![]() b,
b,![]() ,
,
则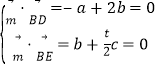 ,取
,取![]() ,得
,得![]() 1,
1,![]() ,
,
![]() 二面角
二面角![]() 大于
大于![]() ,
,
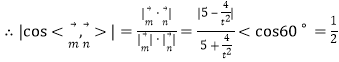 ,
,
解得![]() ,
,
![]() ,
,
![]() 四棱锥
四棱锥![]() 体积
体积![]()
![]() 四棱锥
四棱锥![]() 体积的取值范围是
体积的取值范围是![]()

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】某种蔬菜从1月1日起开始上市,通过市场调查,得到该蔬菜种植成本![]() (单位:元/
(单位:元/![]() )与上市时间
)与上市时间![]() (单位:10天)的数据如下表:
(单位:10天)的数据如下表:
时间 | 5 | 11 | 25 |
种植成本 | 15 | 10.8 | 15 |
(1)根据上表数据,从下列函数:![]() ,
,![]() ,
,![]() ,
,![]() 中(其中
中(其中![]() ),选取一个合适的函数模型描述该蔬菜种植成本
),选取一个合适的函数模型描述该蔬菜种植成本![]() 与上市时间
与上市时间![]() 的变化关系;
的变化关系;
(2)利用你选取的函数模型,求该蔬菜种植成本最低时的上市时间及最低种植成本.