Question

【题目】已知{xn}是各项均为正数的等比数列，且x1＋x2＝3，x3－x2＝2.

(1)求数列{xn}的通项公式；

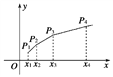
(2)如图，在平面直角坐标系xOy中，依次连接点P1(x1,1)，P(x2,2)，…，Pn＋1(xn＋1，n＋1)得到折线P1P2…Pn＋1，求由该折线与直线y＝0，x＝x1，x＝xn＋1所围成的区域的面积Tn．

Answer 1

【答案】(1)xn＝2n－1．(2) Tn＝．

【解析】试题分析：

（1）根据条件可求得等比数列中x1＝1，q＝2，故可得通项公式为xn＝2n－1．（2）由题意可得梯形PnPn＋1Qn＋1Qn的上下底分别为，高为xn＋1－xn＝2n－1，故可得梯形的面积，并记为bn，则，然后根据错位相减法求和即可．

试题解析：

(1)设等比数列{xn}的公比为q．

由题意得

消去x得3q2－5q－2＝0．

又q>0，

解得q＝2，

∴x1＝1．

∴数列{xn}的通项公式为xn＝2n－1．

(2)过P1，P2，…，Pn＋1向x轴作垂线，垂足分别为Q1，Q2，…，Qn＋1．

由(1)得xn＋1－xn＝2n－2n－1＝2n－1．

记梯形PnPn＋1Qn＋1Qn的面积为bn，则．

∴Tn＝3×2－1＋5×20＋7×21＋…＋(2n－1)×2n－3＋(2n＋1)×2n－2， ①

又2Tn＝3×20＋5×21＋7×22＋…＋(2n－1)×2n－2＋(2n＋1)×2n－1， ②

①－②得

－Tn＝3×2－1＋(2＋22＋…＋2n－1)－(2n＋1)×2n－1

，

∴．