题目内容
【题目】某市为了改善居民的休闲娱乐活动场所,现有一块矩形![]() 草坪如下图所示,已知:
草坪如下图所示,已知:![]() 米,
米,![]() 米,拟在这块草坪内铺设三条小路
米,拟在这块草坪内铺设三条小路![]() 、
、![]() 和
和![]() ,要求点
,要求点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 时上,且
时上,且![]() .
.
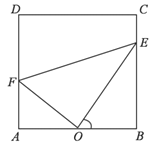
(1)设![]() ,试求
,试求![]() 的周长
的周长![]() 关于
关于![]() 的函数解析式,并求出此函数的定义域;
的函数解析式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为![]() 元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
【答案】(1)![]() ,定义域为
,定义域为![]() ;
;
(2)当![]() 米时,铺路总费用最低,最低总费用为
米时,铺路总费用最低,最低总费用为![]() 元.
元.
【解析】
(1)利用勾股定理通过![]() ,得出
,得出![]() ,结合实际情况得出该函数的定义域;
,结合实际情况得出该函数的定义域;
(2)设![]() ,由题意知,要使得铺路总费用最低,即为求
,由题意知,要使得铺路总费用最低,即为求![]() 的周长
的周长![]() 最小,求出
最小,求出![]() 的取值范围,根据该函数的单调性可得出
的取值范围,根据该函数的单调性可得出![]() 的最小值.
的最小值.
(1)由题意,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
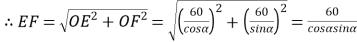 ,
,
所以![]() ,即
,即![]() .
.
当点![]() 在点
在点![]() 时,这时角
时,这时角![]() 最小,求得此时
最小,求得此时![]() ;
;
当点![]() 在
在![]() 点时,这时角
点时,这时角![]() 最大,求得此时
最大,求得此时![]() .
.
故此函数的定义域为![]() ;
;
(2)由题意知,要求铺路总费用最低,只需要求![]() 的周长
的周长![]() 的最小值即可.
的最小值即可.
由(1)得![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,
则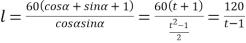 ,
,
由![]() ,得
,得![]() ,
,![]() ,则
,则![]() ,
,
从而![]() ,当
,当![]() ,即当
,即当![]() 时,
时,![]() ,
,
答:当![]() 米时,铺路总费用最低,最低总费用为
米时,铺路总费用最低,最低总费用为![]() 元.
元.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目