题目内容
(本小题满分12分)
已知函数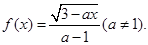
(I)若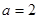 ,求
,求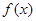 的定义域;
的定义域;
(II) 若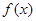 在区间
在区间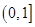 上是减函数,求实数
上是减函数,求实数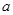 的取值范围.
的取值范围.
已知函数
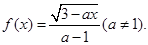
(I)若
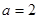 ,求
,求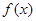 的定义域;
的定义域;(II) 若
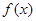 在区间
在区间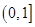 上是减函数,求实数
上是减函数,求实数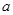 的取值范围.
的取值范围.解:(1)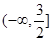 …………………………………………………………………3分
…………………………………………………………………3分
(2) 当 时,由题意知
时,由题意知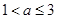 ;……………………………………………6分
;……………………………………………6分
当 时,为增函数,不合;……………………………………………8分
时,为增函数,不合;……………………………………………8分
当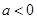 时,
时,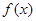 在区间
在区间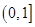 上是减函数………………………………11分
上是减函数………………………………11分
综上可得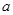 的取值范围是
的取值范围是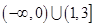 …………………………………………12分
…………………………………………12分
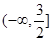 …………………………………………………………………3分
…………………………………………………………………3分(2) 当
 时,由题意知
时,由题意知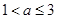 ;……………………………………………6分
;……………………………………………6分当
 时,为增函数,不合;……………………………………………8分
时,为增函数,不合;……………………………………………8分当
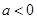 时,
时,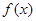 在区间
在区间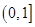 上是减函数………………………………11分
上是减函数………………………………11分综上可得
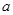 的取值范围是
的取值范围是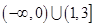 …………………………………………12分
…………………………………………12分略

练习册系列答案
相关题目
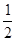 f(x)的是 ( )
f(x)的是 ( )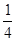
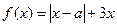 ,其中
,其中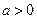 。
。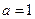 时,求不等式
时,求不等式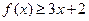 的解集;
的解集;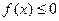 的解集为
的解集为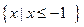 ,求a的值。
,求a的值。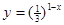
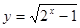
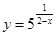
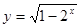
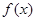 与
与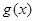 相等( )
相等( )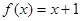 ,
,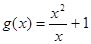
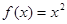 ,
,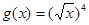
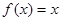 ,
,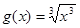
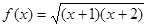 ,
,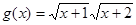
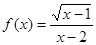 的定义域为( )
的定义域为( ) 如图,现有一块矩形空地,要在这块空地上开辟一个内
如图,现有一块矩形空地,要在这块空地上开辟一个内 接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知
接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知 ,
,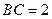 ,且
,且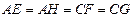 ,设
,设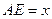 ,绿地面积为
,绿地面积为 .
.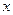 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;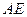 为何值时,绿地面积
为何值时,绿地面积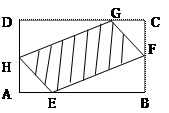
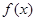 是奇函数,且
是奇函数,且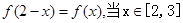 时,
时,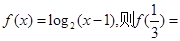 ( )
( )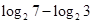 ............
............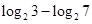
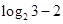 ..........
..........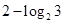
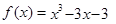 有零点的区间是( )
有零点的区间是( )