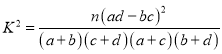题目内容
【题目】已知三棱锥的两条棱长为1，其余四条棱长为2，有下列命题：
该三棱锥的体积是
；
该三棱锥内切球的半径是
；
该三棱锥外接球的表面积是
．
其中正确的是
A. 
B. 
C. 
D. 
【答案】B
【解析】
三棱锥
中,
，
，取BC，PA的中点D，E，①利用过BC中点D与BC垂直的截面三角形PAD为底，以BC高求得体积，验证正确；
②利用四面全等，由内切球球心为顶点把三棱锥等分四份，不难求得半径r，验证正确；
③首先确定DE中点为外接球球心，不难求解，验证错误.
如图所示，三棱锥中
，，
取BC，PA的中点D，E，作如图的连接
则
，
，
平面PAD
并求得：
；
，
三棱锥的体积为
，
正确；
设内切球的半径为r，球心为M，
显然四个面三角形全等
，
解得
，
正确；
事实上，外接球球心O必在过D点与BC垂直的平面PAD内，
和过E点与PA垂直的平面BCE内，
故O点在平面PAD和平面BCE的交线DE上，
在
内，
同样，在
内，
≌
，即O为DE的中点，
可求得外接球半径R的平方：
故
错误
故选：B．
名校联盟快乐课堂系列答案
黄冈创优卷系列答案【题目】为了了解青少年的肥胖是否与常喝碳酸饮料有关，现对30名青少年进行调查，得到如下列联表：
常喝 | 不常喝 | 总计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
总计 | 30 |
已知从这30名青少年中随机抽取1名，抽到肥胖青少年的概率为
．
（1）请将列联表补充完整；（2）是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关？
独立性检验临界值表：
P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式：
，其中n=a+b+c+d．
【题目】独立性检验中,假设
:运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得
的观测值
.下列结论正确的是（ ）
附：
| 0．10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动有关
B. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动无关
C. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动有关
D. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动无关
【题目】近期中央电视台播出的《中国诗词大会》火遍全国，下面是组委会在选拔赛时随机抽取的100名选手的成绩，按成绩分组，得到的频率分布表如下所示.
题号 | 分组 | 频数 | 频率 |
第1组 |
| 0.100 | |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
第6组 |
| 100 | 1.00 |
（1）请先求出频率分布表中①、②位置的相应数据，再完成如下的频率分布直方图；
（2）组委会决定在5名（其中第3组2名，第4组2名，第5组1名）选手中随机抽取2名选接受
考官进行面试，求第4组至少有1名选手被考官面试的概率.
