题目内容
【题目】中心在原点，焦点在x轴上的一椭圆与一双曲线有共同的焦点F1，F2，且|F1F2|＝
，椭圆的长半轴与双曲线实半轴之差为4，离心率之比为3∶7.
（1）求这两曲线的方程；
（2）若P为这两曲线的一个交点，求cos∠F1PF2的值.
【答案】（1）
和
；（2）
【解析】试题分析：（1）设椭圆长、短半轴长分别为
，双曲线半实、虚轴长分别为
，列出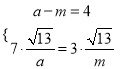
，解出参数的值，即可得出椭圆与双曲线的方程；（2）不妨设
分别为左、右焦点， 
是第一象限的一个交点，则
， 
，再利用余弦定理得出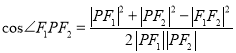
，求值即可.
试题解析：（1）由题意知，半焦距
，设椭圆长半轴为
，则双曲线实半轴
，离心率之比为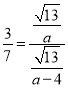
，∴
，∴椭圆的短半轴等于
，双曲线虚半轴的长为
，∴椭圆和双曲线的方程分别为： 
和
.
（2）由椭圆的定义得： 
，由双曲线的定义得： 
，∴
与
中，一个是10，另一个是 4，不妨令
， 
，又
，三角形
中，利用余弦定理得： 
，∴
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
