题目内容
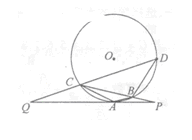
已知PQ与圆O相切于点A,直线PBC交圆于B、C两点,D是圆上一点,且AB∥CD,DC的延长线交PQ于点Q.
(1)求证: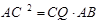
(2)若AQ=2AP,AB=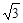 ,BP=2,求QD.
,BP=2,求QD.
(1)求证:
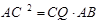
(2)若AQ=2AP,AB=
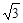 ,BP=2,求QD.
,BP=2,求QD.
(1)证明过程详见解析;(2)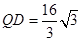 .
.
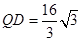 .
.试题分析:本题主要考查同位角、弦切角、相似三角形、切线的性质、切割线定理等基础知识,考查学生的逻辑推理能力、分析问题解决问题的能力、转化能力.第一问,先利用同位角相等得到∠PAB=∠AQC,再利用弦切角相等,得到
 ,同理,AQ为切线,则∠QAC=∠CBA,所有得到三角形相似,利用相似得性质得边的比例关系;第二问,由AB//CQ,利用平行线的性质得
,同理,AQ为切线,则∠QAC=∠CBA,所有得到三角形相似,利用相似得性质得边的比例关系;第二问,由AB//CQ,利用平行线的性质得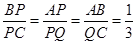 ,得到QC和PC的长,利用切线的性质,得
,得到QC和PC的长,利用切线的性质,得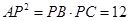 ,
,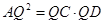 ,得到QD的值.
,得到QD的值.(1)因为AB∥CD,所以∠PAB=∠AQC, 又PQ与圆O相切于点A,所以∠PAB=∠ACB,
因为AQ为切线,所以∠QAC=∠CBA,所以△ACB∽△CQA,所以
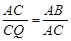 ,
,所以
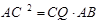 5分
5分(2)因为AB∥CD,AQ=2AP,所以
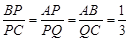 ,由AB=
,由AB=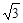 ,BP=2得
,BP=2得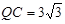 ,PC=6
,PC=6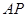 为圆O的切线
为圆O的切线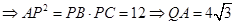
又因为
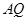 为圆O的切线
为圆O的切线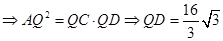 10分
10分
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目

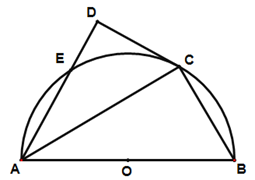
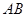 为半圆
为半圆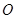 的直径,
的直径,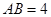 ,
,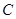 为半圆上一点,过点
为半圆上一点,过点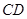 ,过
,过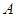 点作
点作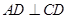 于
于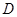 ,交半圆于点
,交半圆于点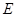 ,
,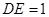 .
.
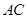 平分
平分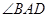 ;
;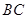 的长.
的长. 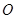 的两弦
的两弦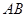 和
和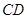 交于点
交于点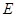 ,
,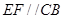 ,
,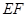 交
交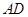 的延长线于点
的延长线于点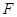 .求证:△
.求证:△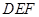 ∽△
∽△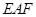 .
.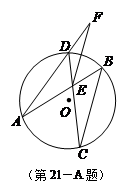
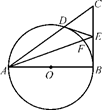

 是圆的内接三角形,
是圆的内接三角形, 的平分线交圆于点
的平分线交圆于点 ,交
,交 于点
于点 ,过点
,过点 的圆的切线与
的圆的切线与 的延长线交于点
的延长线交于点 .在上述条件下,给出下列四个结论:
.在上述条件下,给出下列四个结论:

 ,则CD=________.
,则CD=________.
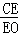 的值为 _________ .
的值为 _________ .