题目内容
【题目】某商场拟对某商品进行促销,现有两种方案供选择,每种促销方案都需分两个月实施,且每种方案中第一个月与第二个月的销售相互独立.根据以往促销的统计数据,若实施方案1,预计第一个月的销量是促销前的1.2倍和1.5倍的概率分别是0.6和0.4,第二个月的销量是第一个月的1.4倍和1.6倍的概率都是0.5;若实施方案2,预计第一个月的销量是促销前的1.4倍和1.5倍的概率分别是0.7和0.3,第二个月的销量是第一个月的1.2倍和1.6倍的概率分别是0.6和0.4.令![]() 表示实施方案
表示实施方案![]() 的第二个月的销量是促销前销量的倍数.
的第二个月的销量是促销前销量的倍数.
(Ⅰ)求![]() ,
, ![]() 的分布列;
的分布列;
(Ⅱ)不管实施哪种方案, ![]() 与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
与第二个月的利润之间的关系如下表,试比较哪种方案第二个月的利润更大.
![]()
【答案】(Ⅰ)见解析;(Ⅱ)实施方案1.
【解析】试题分析:(I)利用两个月销量的倍数两两相乘,求得![]() ,
, ![]() 的所有取值,再利用相互独立事件概率计算公式求得每个取值对应的概率的值,由此求得分布列.(II)根据(I)求得的分布列,求得每个月利润的值和对应的概率,由此求得两个方案利润的分布列,进而求得期望值,比较两个期望值即可得出利润更大的方案.
的所有取值,再利用相互独立事件概率计算公式求得每个取值对应的概率的值,由此求得分布列.(II)根据(I)求得的分布列,求得每个月利润的值和对应的概率,由此求得两个方案利润的分布列,进而求得期望值,比较两个期望值即可得出利润更大的方案.
试题解析:
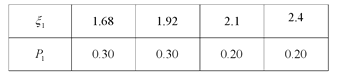
(Ⅰ)依题意, ![]() 的所有取值为1.68,1.92,2.1,2.4,
的所有取值为1.68,1.92,2.1,2.4,
因为![]()
![]() ,
, ![]()
![]() ,
,
![]()
![]() ,
, ![]()
![]() .
.
所以![]() 的分布列为
的分布列为
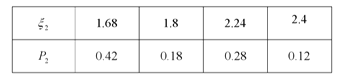
依题意, ![]() 的所有取值为1.68,1.8,2.24,2.4,
的所有取值为1.68,1.8,2.24,2.4,
因为![]()
![]() ,
, ![]()
![]() ,
,
![]()
![]() ,
, ![]()
![]() .
.
所以![]() 的分布列为
的分布列为
(Ⅱ)令![]() 表示方案
表示方案![]() 所带来的利润,则
所带来的利润,则
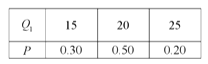
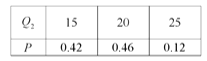
所以![]()
![]()
![]() ,
,
![]()
![]()
![]() .
.
因为![]() ,
,
所以实施方案1,第二个月的利润更大.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目