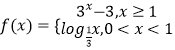题目内容
【题目】已知曲线![]() 为参数),
为参数),![]() 为参数).
为参数).
(1)化![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() 为
为![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() 为参数)距离的最小值.
为参数)距离的最小值.
【答案】(1)C1:(x+4)2+(y﹣3)2=1;C2:![]() ,(2)点Q(
,(2)点Q(![]() ,﹣
,﹣![]() )
)
【解析】试题分析:(1)分别消去两曲线参数方程中的参数得到两曲线的直角坐标方程,即可得到曲线![]() 表示一个圆;曲线
表示一个圆;曲线![]() 表示一个椭圆;(2)把
表示一个椭圆;(2)把![]() 的值代入曲线
的值代入曲线![]() 的参数方程得点
的参数方程得点![]() 的坐标,然后把直线的参数方程化为普通方程,根据曲线
的坐标,然后把直线的参数方程化为普通方程,根据曲线![]() 的参数方程设出
的参数方程设出![]() 的坐标,利用中点坐标公式表示出
的坐标,利用中点坐标公式表示出![]() 的坐标,利用点到直线的距离公式标准处
的坐标,利用点到直线的距离公式标准处![]() 到已知直线的距离,利用两角差的正弦函数公式化简后,利用正弦函数的值域即可得到距离的最小值.
到已知直线的距离,利用两角差的正弦函数公式化简后,利用正弦函数的值域即可得到距离的最小值.
试题解析:(1)![]()
![]() 为圆心是
为圆心是![]() ,半径是1的圆,
,半径是1的圆, ![]() 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在![]() 轴,长半轴长是8,短半轴长是3的椭圆.
轴,长半轴长是8,短半轴长是3的椭圆.
(2)当![]() 时,
时, ![]() ,故
,故![]()
![]() 的普通方程为
的普通方程为![]() ,
, ![]() 到
到![]() 的距离
的距离![]()
所以当![]() 时,
时, ![]() 取得最小值
取得最小值![]() .
.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目