Question

【题目】（本题分）

已知定义在上的两个函数， 图象有公共点，且在公共点处的切线相同．

（Ⅰ）用表示．

（Ⅱ）求证： ．

Answer 1

【答案】详见解析

【解析】试题分析：（Ⅰ）设出两曲线的公共点坐标，分别求出f（x）和g（x）的导函数，把设出点的坐标代入两导函数中得到两关系式，联立两关系式即可解出公共点的横坐标，把求出的横坐标代入得到用a表示出b的式子；

（Ⅱ）设F（x）=f（x）﹣g（x），求出F（x）的导函数，根据导函数的正负得到F（x）的单调区间，由x大于0和函数的增减性得到F（x）的最小值为0，即f（x）﹣g（x）大于等于0，得证．

试题解析：

（Ⅰ）设与公共点处的切线相同．

∵， ，

由题意， ，

即，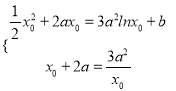

得或（舍去），

即有．

（Ⅱ）证明：设，

则， ，

故在为减函数，在为增函数，

所以函数在上有最小值， ，

故当时，有，

即当时， ．