题目内容
【题目】如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为梯形,AD∥BC,CD⊥BC,AD=2,AB=BC=3,PA=4,M为AD的中点,N为PC上一点,且PC=3PN.
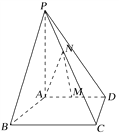
(1)求证:MN∥平面PAB;
(2)求点M到平面PAN的距离.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)作NH∥BC交PB于点H,连接AH,得四边形AMNH为平行四边形,所以MN∥AH,所以MN∥平面PAB;(2)由等体积法得VM-PAC=VP-AMC,即4![]() h=
h=![]() ×4,所以h=
×4,所以h=![]() 。
。
试题解析:
(1)在平面PBC内作NH∥BC交PB于点H,连接AH,
在△PBC中,NH∥BC,且NH=![]() BC=1,AM=
BC=1,AM=![]() AD=1.
AD=1.
又AD∥BC,∴NH∥AM且NH=AM,
∴四边形AMNH为平行四边形,∴MN∥AH,
又AH平面PAB,MN平面PAB,
∴MN∥平面PAB.
(2)连接AC,MC,PM,平面PAN即为平面PAC,设点M到平面PAC的距离为h.
由题意可得CD=2![]() ,AC=2
,AC=2![]() ,
,
∴S△PAC=![]() PA·AC=4
PA·AC=4![]() ,
,
∴S△AMC=![]() AM·CD=
AM·CD=![]() ,
,
由VM-PAC=VP-AMC,得![]() S△PAC·h=
S△PAC·h=![]() S△AMC·PA,
S△AMC·PA,
即4![]() h=
h=![]() ×4,∴h=
×4,∴h=![]() ,
,
∴点M到平面PAN的距离为![]() .
.

 期末集结号系列答案
期末集结号系列答案【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过3S微克/立方米,
的年平均浓度不得超过3S微克/立方米, ![]() 的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天
的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天![]() 的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
组别 |
| 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
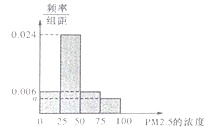
(Ⅰ)将这20天的测量结果按表中分组方法绘制成的样本频率分布直方图如图.
(ⅰ)求图中![]() 的值;
的值;
(ⅱ)在频率分布直方图中估算样本平均数,并根据样本估计总体的思想,从![]() 的年平均度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
的年平均度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
(Ⅱ)将频率视为概率,对于2016年的某3天,记这3天中该居民区![]() 的24小时平均浓度符合环境空气质量标准的天数为
的24小时平均浓度符合环境空气质量标准的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】已知函数f(x)=![]() sinωxcosωx-cos2ωx+
sinωxcosωx-cos2ωx+![]() (ω>0),经化简后利用“五点法”画其在某一周期内的图象时,列表并填入的部分数据如下表:
(ω>0),经化简后利用“五点法”画其在某一周期内的图象时,列表并填入的部分数据如下表:
x | ① |
|
| ||
f(x) | 0 | 1 | 0 | -1 | 0 |
(1)请直接写出①处应填的值,并求函数f(x)在区间![]() 上的值域;
上的值域;
(2)△ABC的内角A,B,C所对的边分别为a,b,c,已知f(A+![]() )=1,b+c=4,a=
)=1,b+c=4,a=![]() ,求△ABC的面积.
,求△ABC的面积.
