题目内容
(本小题15分)设抛物线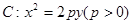 和点
和点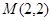 ,.斜率为
,.斜率为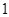 的直线与抛物线
的直线与抛物线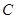 相交不同的两个点
相交不同的两个点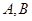 .若点
.若点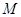 恰好为
恰好为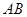 的中点.
的中点.
(1)求抛物线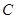 的方程,
的方程,
(2) 抛物线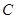 上是否存在异于
上是否存在异于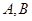 的点
的点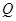 ,使得经过点
,使得经过点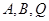 的圆和抛物线
的圆和抛物线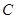 在
在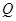 处有相同的切线.若存在,求出点
处有相同的切线.若存在,求出点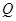 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(1)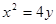 . (2) 存在
. (2) 存在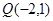
解析试题分析:(1)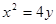 …………………6分
…………………6分
(2)由(1)得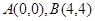 .假设抛物线
.假设抛物线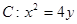 上存在点
上存在点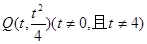
设圆的圆心坐标为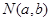 ,则
,则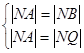 ,
,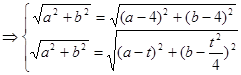
 得
得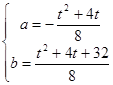 …………………10分
…………………10分
而抛物线在点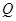 处的斜率为
处的斜率为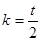 ,又因为
,又因为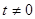 ,且该切线与
,且该切线与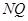 垂直,
垂直,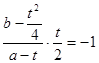
 ,
,
将 代入上式得
代入上式得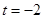 ,故存在
,故存在 …………………15分
…………………15分
考点:本题考查直线与圆锥曲线的基础知识以及抛物线与圆的几何性质。
点评:本题主要考查了直线与圆锥曲线的综合问题,考查学生的基本思想与运算能力、探究能力和推理能力

练习册系列答案
相关题目
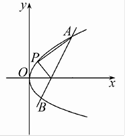
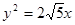 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点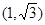 ,又知直线
,又知直线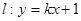 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.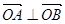 ,求实数k值.
,求实数k值. 的中心,而焦点是双曲线的顶点,求抛物线的方程.
的中心,而焦点是双曲线的顶点,求抛物线的方程.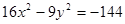 的焦点坐标,离心率和渐近线方程.
的焦点坐标,离心率和渐近线方程.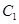 :
: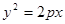 的准线经过双曲线
的准线经过双曲线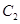 :
: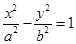 的左焦点,若抛物线
的左焦点,若抛物线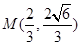 .
.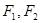 是双曲线
是双曲线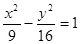 的两个焦点,点
的两个焦点,点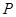 在双曲线上,且
在双曲线上,且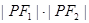
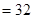 ,求证:
,求证: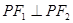
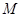 与直线
与直线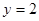 相切,且与定圆
相切,且与定圆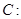
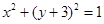 外切,求动圆圆心
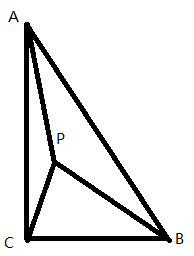
外切,求动圆圆心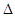 ABC中,
ABC中,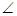 C=90°,AC="b," BC="a," P为三角形内的一点,且
C=90°,AC="b," BC="a," P为三角形内的一点,且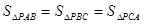 ,
,