题目内容
(10分)已知抛物线的顶点是双曲线 的中心,而焦点是双曲线的顶点,求抛物线的方程.
的中心,而焦点是双曲线的顶点,求抛物线的方程.
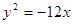 ,
,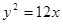 。
。
解析试题分析:首先根据题意,根据双曲线的方程得到其顶点和焦点坐标,进而结合抛物线的标准方程设出,求解得到。注意焦点的位置不定方程也不定,要讨论。
解:由已知: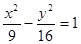 ,
,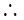 双曲线的顶点为
双曲线的顶点为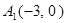
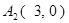 ,
,
若抛物线的焦点为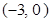 ,则
,则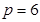 ,所以抛物线的方程为
,所以抛物线的方程为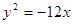
若抛物线的焦点为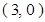 ,则
,则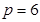 ,所以抛物线的方程为
,所以抛物线的方程为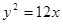 。
。
考点:本题主要考查了双曲线的简单几何性质的运用,和抛物线方程的求解问题。
点评:解决该试题的关键是通过已知的方程确定出双曲线的焦点坐标和顶点坐标,进而得到抛物线的方程的求解问题。

练习册系列答案
相关题目
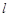 过点(0,3)且与抛物线y2=2x只有一个公共点,求该直线方程.
过点(0,3)且与抛物线y2=2x只有一个公共点,求该直线方程.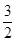 ),两个焦点为(-1,0)(1,0)?
),两个焦点为(-1,0)(1,0)?
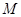 的坐标为
的坐标为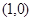 ;
;
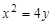 的焦点,且离心率等于
的焦点,且离心率等于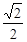 ,直线
,直线 与椭圆C交于M,N两点.
与椭圆C交于M,N两点.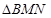 的垂心?若可以,求出直线
的垂心?若可以,求出直线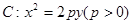 和点
和点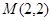 ,.斜率为
,.斜率为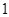 的直线与抛物线
的直线与抛物线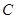 相交不同的两个点
相交不同的两个点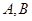 .若点
.若点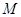 恰好为
恰好为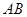 的中点.
的中点.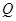 ,使得经过点
,使得经过点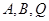 的圆和抛物线
的圆和抛物线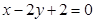 经过椭圆
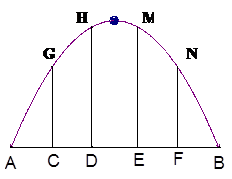
经过椭圆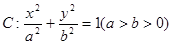 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆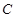 的右顶点为
的右顶点为 ,点
,点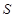 是椭圆
是椭圆 轴上方的动点,直线
轴上方的动点,直线 与直线
与直线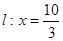 分别交于
分别交于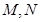 两点。
两点。
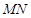 的长度的最小值;
的长度的最小值;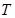 ,使得
,使得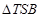 的面积为
的面积为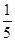 ?若存在,确定点
?若存在,确定点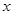 轴上的双曲线
轴上的双曲线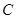 的两条渐近线过坐标原点,且两条渐近线与以
的两条渐近线过坐标原点,且两条渐近线与以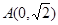 为圆心,1为半径的圆相切,又知
为圆心,1为半径的圆相切,又知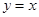 对称.
对称.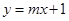 与双曲线
与双曲线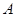 ,
,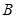 两点,另一直线
两点,另一直线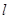 经过
经过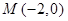 及
及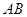 的中点,求直线
的中点,求直线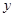 轴上的截距
轴上的截距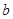 的取值范围.
的取值范围.