题目内容
【题目】已知![]() 为抛物线
为抛物线![]() 的焦点,过点
的焦点,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,抛物线
,抛物线![]() 在
在![]() 两点处的切线分别是
两点处的切线分别是![]() ,且
,且![]() 相交于点
相交于点![]() ,则
,则![]() 的小值是___.
的小值是___.
【答案】6
【解析】
设直线l的方程为:y=kx+1,A(![]() ),B(
),B(![]() ).联立化为:x2﹣4kx﹣4=0,利用根与系数的关系可得|AB|=
).联立化为:x2﹣4kx﹣4=0,利用根与系数的关系可得|AB|=![]() =k(
=k(![]() )+4.对x2=4y两边求导可得:y′
)+4.对x2=4y两边求导可得:y′![]() ,可得切线PA的方程为:y﹣
,可得切线PA的方程为:y﹣![]() (x﹣
(x﹣![]() ),切线PB的方程为:y﹣
),切线PB的方程为:y﹣![]() (x﹣
(x﹣![]() ),联立解得P点坐标,可得代入|PF|
),联立解得P点坐标,可得代入|PF|![]() ,利用导数研究函数的单调性极值即可得出.
,利用导数研究函数的单调性极值即可得出.
设直线l的方程为:y=kx+1,A(![]() ),B(
),B(![]() .
.
联立![]() ,化为:x2﹣4kx﹣4=0,
,化为:x2﹣4kx﹣4=0,
可得:![]() =4k,
=4k,![]() =﹣4,
=﹣4,
|AB|=![]() =k(
=k(![]() )+4=4k2+4.
)+4=4k2+4.
对x2=4y两边求导可得:y′![]() ,
,
可得切线PA的方程为:y﹣![]() (x﹣
(x﹣![]() )
)
切线PB的方程为:y﹣![]() (x﹣
(x﹣![]() ),
),
联立解得:x![]() (
(![]() )=2k,y
)=2k,y![]() =﹣1.∴P(2k,﹣1).
=﹣1.∴P(2k,﹣1).
∴|PF|![]() .
.
∴|PF|![]() ,
,
令![]() t≥2.
t≥2.
则|PF|![]() t
t![]() f(t),
f(t),
f′(t)=1![]() ,当t>4, f′(t)>0;
,当t>4, f′(t)>0;![]() t<4, f′(t)<0
t<4, f′(t)<0
可得t=4时,函数f(t)取得极小值即最小值f(4)=6.当且仅当k![]() 时取等号.
时取等号.
故答案为:6.

【题目】为了检验设备M与设备N的生产效率,研究人员作出统计,得到如下表所示的结果,则
设备M | 设备N | |
生产出的合格产品 | 48 | 43 |
生产出的不合格产品 | 2 | 7 |
附:
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式:![]() ,其中
,其中![]() .
.
A. 有90%的把握认为生产的产品质量与设备的选择有关
B. 没有90%的把握认为生产的产品质量与设备的选择有关
C. 可以在犯错误的概率不超过0.01的前提下认为生产的产品质量与设备的选择有关
D. 不能在犯错误的概率不超过0.1的前提下认为生产的产品质量与设备的选择有关
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量x(万辆) | 100 | 102 | 108 | 114 | 116 |
PM2.5的浓度y(微克/立方米) | 78 | 80 | 84 | 88 | 90 |
(1)根据上表数据,用最小二乘法,求出y关于x的线性回归方程![]() x
x![]() ;
;
(2)若周六同一时间段车流量200万辆,试根据(1)求出的线性回归方程,预测此时PM2.5的浓度为多少?
(参考公式: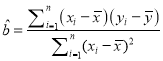 ,
,![]()
![]() ;参考数据:
;参考数据:![]() xi=540,
xi=540,![]() yi=420)
yi=420)

