题目内容
【题目】已知定义在R上的函数f(x)=2x﹣ ![]() .
.
(1)若f(x)= ![]() ,求x的值;
,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
【答案】
(1)解:由题意:f(x)=2x﹣ ![]() 定义在R上的函数,
定义在R上的函数,
∴ 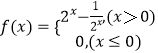
当x≤0时,f(x)=0,无解
当x>0时,f(x)=2x﹣ ![]() ,
,
由f(x)= ![]() ,即:2x﹣
,即:2x﹣ ![]() =
= ![]() ,
,
化简:222x﹣32x﹣2=0
因式分解:(2x﹣2)(22x+2)=0
解得:解得2x=2或2x=﹣ ![]() ,
,
∵2x>0,
故:x=1
(2)解:当t∈[1,2]时,
f(2t)= ![]() ,f(t)=
,f(t)= ![]()
那么: ![]() (
( ![]() )≥0
)≥0
整理得:m(22t﹣1)≥﹣(24t﹣1)
∵22t﹣1>0,∴m≥﹣(22t+1)恒成立即可.
∵t∈[1,2],∴﹣(22t+1)∈[﹣17,﹣5].
要使m≥﹣(22t+1)恒成立,只需m≥﹣5
故:m的取值范围是[﹣5,+∞)
【解析】(1)化简f(x)去掉绝对值,直接进行带值计算即可.(2)求出f(2t),f(t)带入,构造指数函数,利用指数函数的图象及性质对t∈[1,2]恒成立求解.
【考点精析】本题主要考查了函数单调性的判断方法的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能正确解答此题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目