题目内容
【题目】下列各小题中,P是q的充要条件的是(08年山东理改编)
1)p:m<﹣2或m>6;q:y=x2+mx+m+3有两个不同的零点.
2)p: ![]() =1,q:y=f(x)是偶函数.
=1,q:y=f(x)是偶函数.
3)p:cosα=cosβ,q:tanα=tanβ.
4)p:A∩B=A,q:CUBCUA.
【答案】(1)(4)
【解析】解:∵y=x2+mx+m+3有两个不同的零点,
∴△=m2﹣4(m+3>0,解得m<﹣2或m>6.
∴p:“m<﹣2或m>6是q“:“y=x2+mx+m+3有两个不同的零点“的充要条件.故(1)成立.
由 ![]() 可得f(﹣x)=f(x),
可得f(﹣x)=f(x),
但y=f(x)的定义域不一定关于原点对称;故(2)不成立.
3)α=β是tanα=tanβ的既不充分也不必要条件.故(3)不成立.
4)画图可得P是q的充要条件.
所以答案是(1)(4).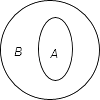

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
