题目内容
5．画出y=|2x2+2x+1|的简图．分析 先求出判别式△＜0，从而对原函数去绝对值并配方可得：$y=2（x+\frac{1}{2}）^{2}+\frac{1}{2}$，由解析式即可看出该二次函数的对称轴及最小值，这样根据对称轴及最小值画出图象即可．
解答 解：△=4-8＜0；
∴2x2+2x+1＞0恒成立；
∴y=2x2+2x+1=$2（x+\frac{1}{2}）^{2}+\frac{1}{2}$；
图象如下：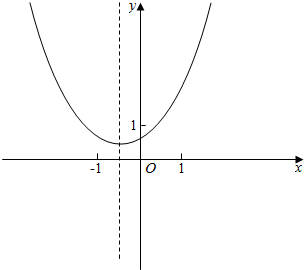
．
点评 考查判别式的符号和二次函数取值的关系，二次函数的对称轴，二次函数的最小值，要熟悉二次函数的图象．
练习册系列答案
相关题目
16．有下列四个命题：
①“若xy=1，则x，y互为倒数”的逆命题；
②“面积相等的三角形全等”的否命题；
③“若m≤1，则x2-2x+m=0有实数解”的逆否命题；
④“若A∩B=B，则A?B”的逆否命题．
其中为真命题的是（ ）
①“若xy=1，则x，y互为倒数”的逆命题；
②“面积相等的三角形全等”的否命题；
③“若m≤1，则x2-2x+m=0有实数解”的逆否命题；
④“若A∩B=B，则A?B”的逆否命题．
其中为真命题的是（ ）
| A． | ①② | B． | ②③ | C． | ④ | D． | ①②③ |
20．
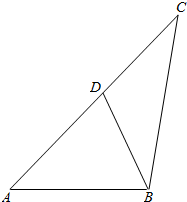如图，在△ABC中，AB=2，AC=4，线段CB的垂直平分线交线段AC于D，AD-DB=1，则△BCD的面积为（ ）
如图，在△ABC中，AB=2，AC=4，线段CB的垂直平分线交线段AC于D，AD-DB=1，则△BCD的面积为（ ）| A． | $\frac{7}{10}$ | B． | $\frac{9}{10}$ | C． | 2 | D． | 8 |
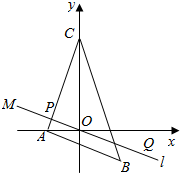如图所示，已知A（-2，0），B（2，-2），C（0，5），过点M（-4，2）且平行于AB的直线l将△ABC分成两部分，求此两部分面积的比值．