题目内容
16.设F1(-c,0),F2(c,0)分别是椭圆E:$\frac{x^2}{a^2}$+${\frac{y}{b^2}^2}$=1(a>b>0)的左、右焦点.(Ⅰ)若点P($\sqrt{3}$,2)在椭圆E上,且c=$\sqrt{3}$,求椭圆E的方程;
(Ⅱ)已知椭圆E的离心率为$\frac{{\sqrt{2}}}{2}$,若过点F1(-c,0)的直线交椭圆E于A,B两点,且|AF1|=3|F1B|.证明:AB⊥AF2.
分析 (Ⅰ)因为F1$(-\sqrt{3},0)$,${F_2}(\sqrt{3},0)$,且点$P(\sqrt{3},2)$在椭圆E上,列式求得椭圆方程.
(Ⅱ)在△AF1F2中和在△ABF2中,分别利用余弦定理求得,再根据条件列出等式求解.
解答 解:(Ⅰ)因为F1$(-\sqrt{3},0)$,${F_2}(\sqrt{3},0)$,且点$P(\sqrt{3},2)$在椭圆E上,
所以$2a=\sqrt{{{(\sqrt{3}+\sqrt{3})}^2}+{{(2-0)}^2}}+\sqrt{{{(\sqrt{3}-\sqrt{3})}^2}+{{(2-0)}^2}}=6,a=3$.
因此b2=a2-c2=9-3=6.故椭圆E的方程为$\frac{x^2}{9}+\frac{y^2}{6}=1$.…(5分)
(Ⅱ)因为$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$,所以$a=\sqrt{2}c$.设|F1B|=t(t>0),则|AF1|=3t,|AB|=4t.
在△AF1F2中,$cosA=\frac{{{{(3t)}^2}+{{(2a-3t)}^2}-{{(2c)}^2}}}{2×3t×(2a-3t)}=\frac{{9{t^2}+{{(2a-3t)}^2}-2{a^2}}}{2×3t×(2a-3t)}$,
在△ABF2中,$cosA=\frac{{{{(4t)}^2}+{{(2a-3t)}^2}-{{(2a-t)}^2}}}{2×4t×(2a-3t)}=\frac{{16{t^2}+{{(2a-3t)}^2}-{{(2a-t)}^2}}}{2×4t×(2a-3t)}$…(10分)
所以$\frac{{9{t^2}+{{(2a-3t)}^2}-2{a^2}}}{2×3t×(2a-3t)}$=$\frac{{16{t^2}+{{(2a-3t)}^2}-{{(2a-t)}^2}}}{2×4t×(2a-3t)}$,整理得,3at=a2,a=3t.
于是|AF2|=3t=|AF1|,|BF2|=5t,|AB|=4t,∠A=90°,故AB⊥AF2.…(13分)
点评 本题主要考查求椭圆方程的方法和利用余弦定理解决综合问题得能力,属于中档题,再高考中时常涉及.

 53随堂测系列答案
53随堂测系列答案| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
| A. | $\frac{3}{2}$e${\;}^{\frac{2}{3}}$ | B. | $\frac{13}{6}$e6 | C. | $\frac{1}{6}$e6 | D. | $\frac{7}{2}$e${\;}^{\frac{2}{3}}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
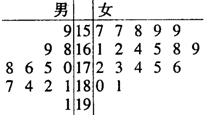 2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.
2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.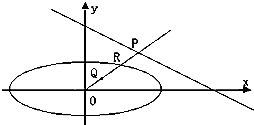 已知椭圆C:$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{16}$=1,直线l:$\frac{x}{12}$+$\frac{y}{8}$=1.
已知椭圆C:$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{16}$=1,直线l:$\frac{x}{12}$+$\frac{y}{8}$=1. 如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A、B、C、D.记λ=$\frac{m}{n}$,△BDM和△ABN的面积分别为S1和S2.
如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A、B、C、D.记λ=$\frac{m}{n}$,△BDM和△ABN的面积分别为S1和S2.