题目内容
在极坐标系中,点P(2,
)到直线ρsin(θ-
)=1的距离等于( )A.1
B.2
C.3
D.1+3
解法一:∵xP=2cos=
,yP=2sin
=-1,?
∴P点的直角坐标为(
,-1).?
又直线ρsin(θ-
)=1化为直角坐标方程为
y-
x-1=0.?
∴P点到直线的距离为d=|-
-
·
-1|=1+
.
解法二:直线ρsin(θ-
)=1与直线θ=
平行,且距离为1.?
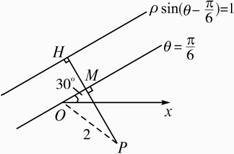
过P点作PH垂直于直线
ρsin(θ-
)=1,垂足为H,设PH交直线θ=
于M,在Rt△POM中,OP=2,∠POM=
.?
∴PM=2sin
=
.?
故P点到直线ρsin(θ-
)=1的距离为1+
.
答案:D
练习册系列答案
怎样学好牛津英语系列答案
相关题目
A．（坐标系与参数方程选做题）在极坐标系中，点在极坐标系中，点P（ρ，θ）关于极点对称的点的一个坐标是（ ）
| A、（-ρ，-θ） | B、（ρ，-θ） | C、（ρ，π-θ） | D、（ρ，π+θ） |