题目内容
A．（坐标系与参数方程选做题）在极坐标系中，点P(2，| 3π |
| 2 |
1
1
． B．（几何证明选讲选做题）已知PA是圆O的切线，切点为A，PA=2，AC是圆O的直径，PC与圆O交于点B，PB=1，则圆O的半径R的长为
| 3 |
| 3 |
分析：A．求出在直角坐标系中点P和直线l的普通方程，由此能求出P到l的距离．
B．由PA是⊙O的切线，知∠PAB=∠C，由∠APB=∠CPA，知△PAB∽△PCA，由此能求出圆O的半径R的长．
B．由PA是⊙O的切线，知∠PAB=∠C，由∠APB=∠CPA，知△PAB∽△PCA，由此能求出圆O的半径R的长．
解答：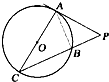
A．解：极坐标系中的点P(2，
)在直角坐标系中为P（0，-2），
∵直线l：3ρcosθ-4ρsinθ=3，
直线l的普通方程：3x-4y-3=0，
所以P到l的距离：d=
=1．
故答案为：1．
B．解：如图，∵PA是⊙O的切线，
∴∠PAB=∠C，
又∵∠APB=∠CPA，∴△PAB∽△PCA，
∴
=
，即
=
，
∴R=
=
=
．
故答案为：
．
A．解：极坐标系中的点P(2，| 3π |
| 2 |
∵直线l：3ρcosθ-4ρsinθ=3，
直线l的普通方程：3x-4y-3=0，
所以P到l的距离：d=
| |3×0-4×(-2)-3| | ||
|
故答案为：1．
B．解：如图，∵PA是⊙O的切线，
∴∠PAB=∠C，
又∵∠APB=∠CPA，∴△PAB∽△PCA，
∴
| PA |
| AC |
| PB |
| AB |
| PA |
| 2R |
| PB |
| AB |
∴R=
| PA•AB |
| 2PB |
2×
| ||
| 2×1 |
| 3 |
故答案为：
| 3 |
点评：第A题考查极坐标方程与普通方程的互化，是基础题．解题时要认真审题，注意点到直线距离公式的应用．
第B题考查与圆有关的比例线段的应用，解题时要认真审题，仔细解答，注意到三角形相似的灵活运用．
第B题考查与圆有关的比例线段的应用，解题时要认真审题，仔细解答，注意到三角形相似的灵活运用．
练习册系列答案
相关题目
选做题（请考生在三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）
（考生注意：只能从下列A、B、C三题中选做一题，如果多做，则按第一题评阅记分）
A：（坐标系与参数方程选做题）在极坐标系中，由θ=0，θ=