题目内容
在极坐标系中，点P（2，π）与点Q关于射线θ=| 2π | 3 |
分析：先根据题意画出极坐标，求|PQ|可转化成求PM的长，在直角三角形PMO中求解即可．
解答：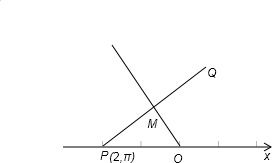
解：根据题意画出图形
∠POM=60°，PO=2，∴PM=
PQ=2PM=2
故答案为2
解：根据题意画出图形∠POM=60°，PO=2，∴PM=
| 3 |
PQ=2PM=2
| 3 |
故答案为2
| 3 |
点评：本题主要考查了极坐标，以及点关于直线的对称问题，属于基础题．
练习册系列答案
相关题目
A．（坐标系与参数方程选做题）在极坐标系中，点在极坐标系中，点P（ρ，θ）关于极点对称的点的一个坐标是（ ）
| A、（-ρ，-θ） | B、（ρ，-θ） | C、（ρ，π-θ） | D、（ρ，π+θ） |