Question

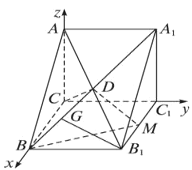
【题目】如图，直三棱柱ABC—A1B1C1中，∠ACB=90°，AC=AA1=1，, AB1与A1B相交于点D，M为B1C1的中点 .

（1）求证：CD⊥平面BDM；

（2）求平面B1BD与平面CBD所成锐二面角的余弦值.

Answer 1

【答案】(1)见解析 (2)

【解析】

（1）先以CB为x轴，CC1为y轴，CA为z轴建立空间直角坐标系，然后分别确定点B、M、D的坐标，利用向量法证明CD⊥平面BDM．（2）求出平面BDC的法向量和平面B1BD的法向量，利用向量法能求出平面B1BD与平面CBD所成锐二面角余弦值．

证明：（1）由题意知AC、BC、CC1两两垂直，

则以CB为x轴，CC1为y轴，CA为z轴建立空间直角坐标系．

∵CB，CC1＝AA1＝1，CA＝1，M为B1C1的中点．

∴B（，0，0），M（，1，0），

又∵点D是矩形AA1B1B的两条对角线的交点，

∴D（，，），

则（），（，1，0），（，），

∴，0，

∴CD⊥BM，CD⊥BD，

又BM∩BD＝B，∴CD⊥平面BDM．

（2）由（1）

（），（），

设平面BDC的法向量（x，y，z），

则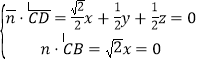，取y＝1，得（0，1，﹣1），

B1（，1，0），（，），（0，1，0），

设平面B1BD的法向量（a，b，c），

则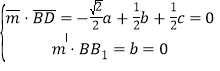，取a＝1，得（1，0，），

设平面B1BD与平面CBD所成锐二面角为θ，

则cosθ．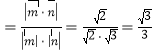

∴平面B1BD与平面CBD所成锐二面角的余弦值为．