Question

【题目】甲、乙两人玩转盘游戏，该游戏规则是这样的：一个质地均匀的标有12等分数字格的转盘（如图），甲、乙两人各转转盘一次，转盘停止时指针所指的数字为该人的得分．（假设指针不能指向分界线）现甲先转，乙后转，求下列事件发生的概率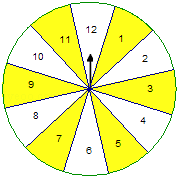

（1）甲得分超过7分的概率．
（2）甲得7分，且乙得10分的概率
（3）甲得5分且获胜的概率．

Answer 1

【答案】
（1）解：甲先转，甲得分超过（7分）为事件A，

记事件A1：甲得（8分），记事件A2：甲得（9分），

记事件A3：甲得（10分），记事件A4：甲得（11分），

记事件A5：甲得（12分），

由几何概型求法，以上事件发生的概率均为 ，

甲得分超过（7分）为事件A，A=A1∪A2∪A3∪A4∪A5

P（A）=P（A1∪A2∪A3∪A4∪A5）=

（2）解：记事件C：甲得（7分）并且乙得（10分），

以甲得分为x，乙得分为y，组成有序实数对（x，y），可以发现，x=1的数对有12个，同样x等于2，3，4，5，6，7，8，9，10，11，12的数对也有12个，所以这样的有序实数对（x，y）有144个，

其中甲得（7分），乙得（10分）为（7，10）共1个，P（C）=

（3）解：甲先转，得（5分），且甲获胜的基本事件为（5，4）（5，3）（5，2）（5，1）

则甲获胜的概率P（D）=

【解析】（1）甲先转，甲得分超过（7分）为事件A，记事件A1：甲得（8分），记事件A2：甲得（9分），记事件A3：甲得（10分），记事件A4：甲得（11分），记事件A5：甲得（12分），由几何概型求法，即可求得甲得分超过7分的概率．（2）记事件C：甲得（7分）并且乙得（10分），以甲得分为x，乙得分为y，组成有序实数对（x，y），可以发现，x=1的数对有12个，同样x等于2，3，4，5，6，7，8，9，10，11，12的数对也有12个，所以由古典概型求法，即可求得甲得分超过7分的概率；（3）甲先转，得（5分），且甲获胜的基本事件为（5，4）（5，3）（5，2）（5，1）由古典概型求法，即可求得甲获胜的概率．