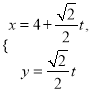جâؤ؟ؤعبف
،¾جâؤ؟،؟ؤ³س،ث¢³§خھءثرذ¾؟س،ث¢µ¥²لتé¼®µؤ³ة±¾y£¨µ¥خ»£؛شھ£©سëس،ث¢²لتx£¨µ¥خ»£؛ا§²ل£©ض®¼نµؤ¹طدµ£¬شعس،ضئؤ³ضضتé¼®ت±½ّذذءثح³¼ئ£¬دà¹طت¾ف¼ûدآ±ي£؛

¸ù¾فزشةدت¾ف£¬¼¼تُبثش±·ض±ً½èضْ¼×،¢ززء½ضض²»ح¬µؤ»ط¹éؤ£ذح£¬µأµ½ءثء½¸ِ»ط¹é·½³ج£¬¼×£؛ ![]()
خھءثئہ¼غء½ضضؤ£ذحµؤؤâ؛دذ§¹û£¬حê³ةزشدآبخخٌ£؛
£¨1£©£¨¢،£©حê³ةدآ±ي£¨¼ئثم½ل¹û¾«ب·µ½0.1£©£؛

£¨¢¢£©·ض±ً¼ئثمؤ£ذح¼×سëؤ£ذحززµؤ²ذ²îئ½·½؛ح![]() ¼°
¼°![]() £¬²¢ح¨¹±ب½د
£¬²¢ح¨¹±ب½د![]() ,
,![]() µؤ´َذ،£¬إذ¶دؤؤ¸ِؤ£ذحؤâ؛دذ§¹û¸ü؛أ.
µؤ´َذ،£¬إذ¶دؤؤ¸ِؤ£ذحؤâ؛دذ§¹û¸ü؛أ.
£¨2£©¸أتéةدتذ؛َ£¬تـµ½¹م´َ¶ءصكµؤببءز»¶س£¬²»¾أ±مب«²؟تغَہ£¬سعتاس،ث¢³§¾ِ¶¨½ّذذ¶´خس،ث¢£¬¸ù¾فتذ³،µ÷²é£¬ذآذèاَء؟خھ8ا§²ل£¨¸إآتخھ0.8£©»ٍ10ا§²ل£¨¸إآتخھ0.2£©£¬بôس،ث¢³§زشأ»²â5شھµؤ¼غ¸ٌ½«تé¼®³ِتغ¸ّ¶©»ُةج£¬ختس،ث¢³§¶´خس،ث¢8ا§²ل»¹تا10ا§²ل؛م»ٌµأ¸ü¶àµؤہûبَ£؟£¨°´£¨1£©ضذؤâ؛دذ§¹û½د؛أµؤؤ£ذح¼ئثمس،ث¢µ¥²لتéµؤ³ة±¾£©
،¾´ً°¸،؟£¨1£©(¢،)¼û½âخِ(¢¢)ؤ£ذحززµؤؤâ؛دذ§¹û¸ü؛أ£®£¨2£©س،ث¢8ا§²ل¶شس،ث¢³§¸üسذہû£®
،¾½âخِ،؟تشجâ·ضخِ£؛£¨1£©(¢،)¸ù¾ف¹«ت½¼ئثم£¬جîبë¶شس¦±ي¸ٌ(¢¢) ±ب½د²ذ²îئ½·½؛ح´َذ،£¬ش½ذ،ش½؛أ£¬¹تؤ£ذحززµؤؤâ؛دذ§¹û¸ü؛أ£®£¨2£©·ض±ً¼ئثمس،ث¢8ا§²لسë10ا§²لµؤہûبَ£؛¶´خس،ث¢8ا§²ل£¬شٍس،ث¢³§»ٌہûخھ![]() (شھ)£¬ب綴خس،ث¢10ا§²ل£¬شٍأ؟²ل³ة±¾خھ
(شھ)£¬ب綴خس،ث¢10ا§²ل£¬شٍأ؟²ل³ة±¾خھ![]() £¬ذèاَئعحûضµخھ
£¬ذèاَئعحûضµخھ![]() £®زٍ¶ّ»ٌہûخھ
£®زٍ¶ّ»ٌہûخھ![]() £¬ةظسعس،ث¢8ا§²ل»ٌµؤہûبَ.
£¬ةظسعس،ث¢8ا§²ل»ٌµؤہûبَ.
تشجâ½âخِ£؛½â£؛(¢ٌ) (¢،) ¾¼ئثم£¬؟ةµأدآ±ي£®
س،ث¢²لت | 2 | 3 | 4 | 5 | 8 | |
µ¥²ل³ة±¾ | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
ؤ£ذح¼× | ¹ہ¼ئضµ | 3.1 | 2.4 | 2.1 | 1.9 | 1.6 |
²ذ²î | 0.1 | 0 | -0.1 | 0 | 0.1 | |
ؤ£ذحزز | ¹ہ¼ئضµ | 3.2 | 2.3 | 2 | 1.9 | 1.7 |
²ذ²î | 0 | 0.1 | 0 | 0 | 0 | |
(¢¢) ![]() £¬
£¬ ![]() £¬
£¬
![]() £¬¹تؤ£ذحززµؤؤâ؛دذ§¹û¸ü؛أ£®
£¬¹تؤ£ذحززµؤؤâ؛دذ§¹û¸ü؛أ£®
(¢ٍ) بô¶´خس،ث¢8ا§²ل£¬شٍس،ث¢³§»ٌہûخھ![]() (شھ) £®
(شھ) £®
بô¶´خس،ث¢10ا§²ل£¬سة(¢ٌ)؟ةضھ£¬µ¥²لتéس،ث¢³ة±¾خھ![]() (شھ)£¬
(شھ)£¬
¹تس،ث¢×ـ³ة±¾خھ![]() (شھ) £®
(شھ) £®
ةèذآذèاَء؟خھ![]() (ا§²ل)£¬س،ث¢³§ہûبَخھ
(ا§²ل)£¬س،ث¢³§ہûبَخھ![]() (شھ)£¬شٍ
(شھ)£¬شٍ
| 8 | 10 |
| 0.8 | 0.2 |
![]() £®
£®
¹ت![]() £®
£®
¹تس،ث¢8ا§²ل¶شس،ث¢³§¸üسذہû£®

 µ¼ر§سë²âتشدµءذ´ً°¸
µ¼ر§سë²âتشدµءذ´ً°¸ ذآ·ا·²½ج¸¨³ه´ج100·ضدµءذ´ً°¸
ذآ·ا·²½ج¸¨³ه´ج100·ضدµءذ´ً°¸