题目内容
已知p:?x∈R,f(x)=|x-2|+|x|>m恒成立.q:f(x)=log5m-2x在(0,+∞)为单调递增,当¬p、¬q有且仅有一个为真命题时,求m的取值范围.
去掉绝对值可得:f(x)=
,所以f(x)min=2,
因为?x∈R,f(x)=|x-2|+|x|>m恒成立,∴m<2…(4分)
因为:q:f(x)=lo
x在(0,+∞)为单调增函数.
∴5m-2>1即:m>
…(8分)
故¬p是真命题时m≥2,¬q是真命题时m≤
,
因为¬p、¬q有且仅有一个为真命题
所以m的取值范围为:m≥2或m≤
…(12分)
|
因为?x∈R,f(x)=|x-2|+|x|>m恒成立,∴m<2…(4分)
因为:q:f(x)=lo
| g | 5m-2 |
∴5m-2>1即:m>
| 3 |
| 5 |
故¬p是真命题时m≥2,¬q是真命题时m≤
| 3 |
| 5 |
因为¬p、¬q有且仅有一个为真命题
所以m的取值范围为:m≥2或m≤
| 3 |
| 5 |

练习册系列答案
相关题目
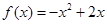 .
.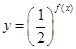 的最小值;
的最小值;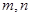 ,当
,当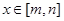 时,
时,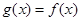 ,且
,且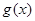 的值域为
的值域为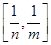 ?若存在,求出所有的
?若存在,求出所有的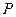 :
: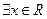 ,使
,使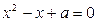 ;命题
;命题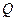 :函数
:函数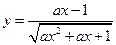 的定义域为R.(1)若命题
的定义域为R.(1)若命题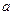 的取值范围;(2)若命题
的取值范围;(2)若命题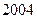 年
年 月
月 日是国庆节,又是中秋节;②
日是国庆节,又是中秋节;②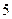 的倍数;
的倍数; 的解
的解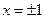 。其中使用逻辑联结词的命题有( )
。其中使用逻辑联结词的命题有( )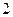 个
个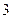 个
个  个
个