题目内容
（本小题满分12分）
如图5所示，在正方体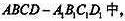
E是棱
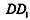的中点。
（Ⅰ）求直线BE的平面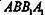
所成的角的正弦值；
（II）在棱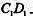
上是否存在一点F，使
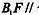平面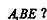
证明你的结论。
如图5所示，在正方体
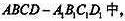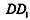E是棱的中点。（Ⅰ）求直线BE的平面
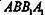所成的角的正弦值；（II）在棱
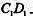上是否存在一点F，使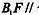平面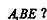证明你的结论。
略
练习册系列答案
名校课堂系列答案
相关题目
题目内容
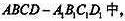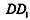E是棱的中点。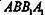所成的角的正弦值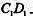；上是否存在一点F，使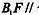平面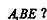证明你的结论。名校课堂系列答案
中，
沿
折起，使平面
⊥平面
.
⊥平面
的大小；
是侧棱
中点，求直线
与平面
所成角的正弦值.
与
都是边长为2的正三角形，
平面
，
平面
.
到平面
的距离；
与平面
中，
、
分别是棱
,
,
与
所成角的余弦值；
平面
的正弦值。
平面ABCD，MA//PB，PB=AB=2MA=2。
面PAC；
（3）求直线BD和平面PMD所成角的正弦值。
的棱长是2，
，
，直线B1C与平面ABC成30°角。
—A的正切值。
是三个不同的平面，命题“
且
”是真命题．若把