题目内容
如图,
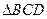 与
与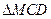 都是边长为2的正三角形,
都是边长为2的正三角形,平面
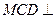 平面
平面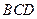 ,
,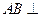 平面
平面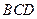 ,
,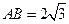 .
.(1)求点
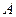 到平面
到平面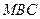 的距离;
的距离;(2)求平面
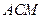 与平面
与平面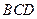 所成二面角的正弦值.
所成二面角的正弦值.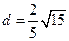 ,
,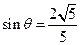
解法一:(1)等体积法.
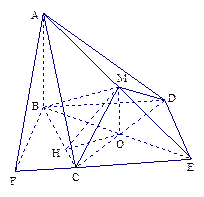
取CD中点O,连OB,OM,则OB=OM=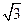 ,OB⊥CD,MO⊥CD.
,OB⊥CD,MO⊥CD.
又平面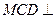 平面
平面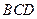 ,则MO⊥平面
,则MO⊥平面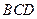 ,所以MO∥AB,MO∥平面ABC.M、O到平面ABC的距离相等.
,所以MO∥AB,MO∥平面ABC.M、O到平面ABC的距离相等.
作OH⊥BC于H,连MH,则MH⊥BC.
求得OH=OC•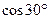 =
=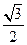 ,
,
MH= .
.
设点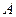 到平面
到平面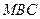 的距离为d,由
的距离为d,由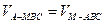 得
得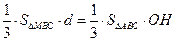 .
.
即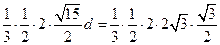 ,
,
解得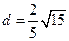 .
.
(2)延长AM、BO相交于E,连CE、DE,CE是平面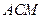 与平面
与平面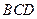 的交线.
的交线.
由(1)知,O是BE的中点,则BCED是菱形.
作BF⊥EC于F,连AF,则AF⊥EC,∠AFB就是二面角A-EC-B的平面角,设为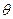 .
.
因为∠BCE=120°,所以∠BCF=60°.
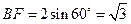 ,
,
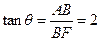 ,
,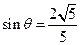 .
.
则所求二面角的正弦值为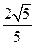
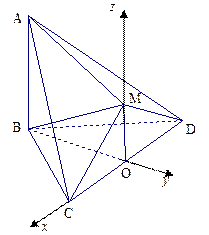
解法二:取CD中点O,连OB,OM,则
OB⊥CD,OM⊥CD.又平面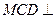 平面
平面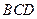 ,则MO⊥平面
,则MO⊥平面 .
.
取O为原点,直线OC、BO、OM为x轴、y轴、z轴,建立空间直角坐标系如图.OB=OM=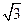 ,则各点坐标分别为C(1,0,0),M(0,0,
,则各点坐标分别为C(1,0,0),M(0,0,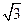 ),B(0,
),B(0,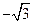 ,0),A(0,-
,0),A(0,-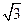 ,
,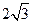 ).
).
(1)设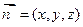 是平面MBC的法向量,则
是平面MBC的法向量,则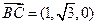 ,
,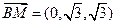 .
.
由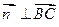 得
得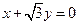 ;
;
由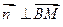 得
得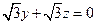 .
.
取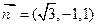 .
.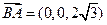 ,则
,则
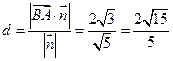 .
.
(2)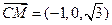 ,
,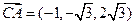 .
.

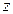 设平面ACM的法向量为
设平面ACM的法向量为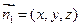 ,由
,由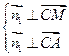 得
得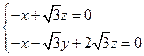 解得
解得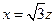 ,
,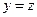 ,取
,取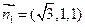 .又平面BCD的法向量为
.又平面BCD的法向量为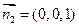 .
.
所以 ,
,
设所求二面角为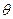 ,则
,则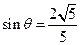 .
.


取CD中点O,连OB,OM,则OB=OM=
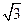 ,OB⊥CD,MO⊥CD.
,OB⊥CD,MO⊥CD.又平面
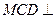 平面
平面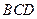 ,则MO⊥平面
,则MO⊥平面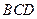 ,所以MO∥AB,MO∥平面ABC.M、O到平面ABC的距离相等.
,所以MO∥AB,MO∥平面ABC.M、O到平面ABC的距离相等.作OH⊥BC于H,连MH,则MH⊥BC.
求得OH=OC•
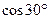 =
=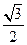 ,
,MH=
 .
.设点
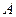 到平面
到平面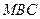 的距离为d,由
的距离为d,由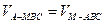 得
得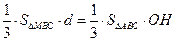 .
.即
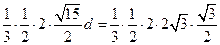 ,
,解得
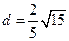 .
.(2)延长AM、BO相交于E,连CE、DE,CE是平面
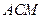 与平面
与平面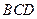 的交线.
的交线.由(1)知,O是BE的中点,则BCED是菱形.
作BF⊥EC于F,连AF,则AF⊥EC,∠AFB就是二面角A-EC-B的平面角,设为
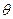 .
.因为∠BCE=120°,所以∠BCF=60°.
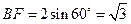 ,
,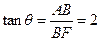 ,
,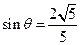 .
.则所求二面角的正弦值为
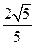
解法二:取CD中点O,连OB,OM,则
OB⊥CD,OM⊥CD.又平面
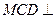 平面
平面 ,则MO⊥平面
,则MO⊥平面 .
.取O为原点,直线OC、BO、OM为x轴、y轴、z轴,建立空间直角坐标系如图.OB=OM=
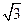 ,则各点坐标分别为C(1,0,0),M(0,0,
,则各点坐标分别为C(1,0,0),M(0,0,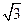 ),B(0,
),B(0,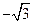 ,0),A(0,-
,0),A(0,-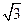 ,
,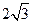 ).
).(1)设
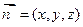 是平面MBC的法向量,则
是平面MBC的法向量,则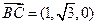 ,
,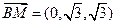 .
.由
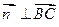 得
得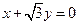 ;
;由
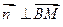 得
得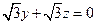 .
.取
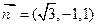 .
.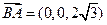 ,则
,则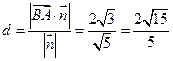 .
.(2)
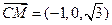 ,
,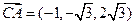 .
.
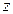 设平面ACM的法向量为
设平面ACM的法向量为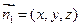 ,由
,由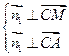 得
得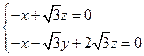 解得
解得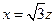 ,
,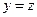 ,取
,取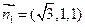 .又平面BCD的法向量为
.又平面BCD的法向量为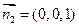 .
.所以
 ,
,设所求二面角为
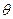 ,则
,则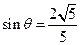 .
.
练习册系列答案
相关题目

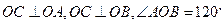 , 且
, 且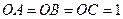
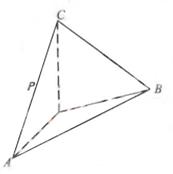
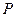 为
为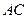 的中点,证明:在
的中点,证明:在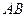 上存在一点
上存在一点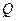 ,使
,使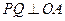 ,并计算
,并计算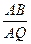 的值;
的值;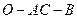 的平面角的余弦值。
的平面角的余弦值。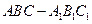 的各棱长都为
的各棱长都为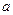 ,
,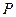 为棱
为棱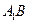 上的动点.
上的动点.
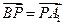 时,求证:
时,求证: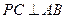 ;
; 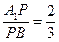 ,求二面角
,求二面角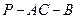 的大小;
的大小; 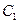 到平面
到平面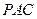 的距离.
的距离.
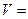 ( )
( )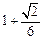
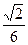
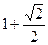
 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是
是一个平面,则下列命题正确的是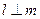 ,
,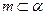 ,则
,则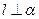
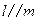 ,则
,则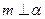
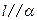 ,
,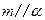 ,则
,则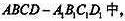 E是棱
E是棱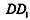 的中点。
的中点。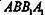 所成的角的正弦值;
所成的角的正弦值;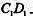 上是否存在一点F,使
上是否存在一点F,使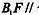 平面
平面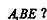 证明你的结论。
证明你的结论。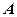 、
、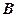 、
、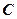 的截面与球心的距离为球半径的一半,且
的截面与球心的距离为球半径的一半,且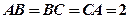 ,则这个球的表面积等于( )
,则这个球的表面积等于( )