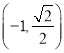题目内容
【题目】函数
图象上不同两点
，
，
，
处的切线的斜率分别是
，
，规定
叫曲线在点
与点
之间的“弯曲度”，给出以下命题：
（1）函数
图象上两点、的横坐标分别为1，2，则
；
（2）存在这样的函数，图象上任意两点之间的“弯曲度”为常数；
（3）设点、是抛物线，
上不同的两点，则
；
（4）设曲线
上不同两点，，，，且
，若
恒成立，则实数
的取值范围是
；
以上正确命题的序号为__（写出所有正确的）
【答案】（2）（3）
【解析】
由新定义，利用导数逐一求出函数
、
在点
与点
之间的“弯曲度”判断（1）、（3）；举例说明（2）正确；求出曲线
上不同两点
，
，
，
之间的“弯曲度”，然后结合
得不等式，举反例说明（4）错误．
解：对于（1），由，得
，
则
，
，
，
，则
，
，（1）错误；
对于（2），常数函数
满足图象上任意两点之间的“弯曲度”为常数，（2）正确；
对于（3），设，，，，
，
则
，
．
，（3）正确；
对于（4），由，得
， 
．
恒成立，即
恒成立，
时该式成立，
（4）错误．
故答案为：（2）（3）．
练习册系列答案
相关题目
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系，某校在高中生中随机抽取100名学生进行了问卷调查，得到如下列联表：
喜欢数学 | 不喜欢数学 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 50 | 100 |
（1）请将上面的列联表补充完整；
（2）能否在犯错误的概率不超过0.001的前提下认为“喜欢数学”与性别有关？说明你的理由；
（3）若在接受调查的所有男生中按照“是否喜欢数学”进行分层抽样，现随机抽取6人，再从6人中抽取3人，求至少有1人“不喜欢数学”的概率.
下面的临界值表供参考：
| 0.05 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 6.635 | 7.879 | 10.828 |
（参考公式：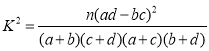
，其中
）.
