题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的零点个数;
的零点个数;
(2)若![]() ,
,![]() ,证明:
,证明:![]() ,
,![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)将a的值代入f(x),再求导得![]() ,在定义域内讨论函数单调性,再由函数的最小值正负来判断它的零点个数;(2)把a的值代入f(x),将
,在定义域内讨论函数单调性,再由函数的最小值正负来判断它的零点个数;(2)把a的值代入f(x),将![]() 整理化简为
整理化简为![]() ,即证明该不等式在
,即证明该不等式在![]() 上恒成立,构造新的函数
上恒成立,构造新的函数![]() ,利用导数可知其在定义域上的最小值,构造函数
,利用导数可知其在定义域上的最小值,构造函数![]() ,由导数可知其定义域上的最大值,二者比较大小,即得证。
,由导数可知其定义域上的最大值,二者比较大小,即得证。
(1)解:因为![]() ,所以
,所以![]() .
.
令![]() ,得
,得![]() 或
或![]() ;令
;令![]() ,得
,得![]() ,
,
所以![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
而![]() ,
,![]() ,
,![]() ,
,
所以![]() 的零点个数为1.
的零点个数为1.
(2)证明:因为![]() ,从而
,从而![]() .
.
又因为![]() ,
,
所以要证![]() ,
,![]() 恒成立,
恒成立,
即证![]() ,
,![]() 恒成立,
恒成立,
即证![]() ,
,![]() 恒成立.
恒成立.
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() .
.
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() 恒成立,
恒成立,
即![]() ,
,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
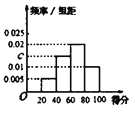
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
(1)由该题中频率分布直方图求测试成绩的平均数和中位数;
(2)其他条件不变,在评定等级为“合格”的学生中依次抽取2人进行座谈,每次抽取1人,求在第1次抽取的测试得分低于80分的前提下,第2次抽取的测试得分仍低于80分的概率;
(3)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.