题目内容
给定抛物线 ,
, 是抛物线
是抛物线 的焦点,过点
的焦点,过点 的直线
的直线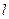 与
与 相交于
相交于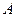 、
、 两点,
两点, 为坐标原点.
为坐标原点.
(1)设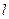 的斜率为1,求以
的斜率为1,求以 为直径的圆的方程;
为直径的圆的方程;
(2)设 ,求直线
,求直线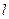 的方程.
的方程.
 ,
, 是抛物线
是抛物线 的焦点,过点
的焦点,过点 的直线
的直线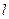 与
与 相交于
相交于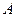 、
、 两点,
两点, 为坐标原点.
为坐标原点.(1)设
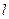 的斜率为1,求以
的斜率为1,求以 为直径的圆的方程;
为直径的圆的方程;(2)设
 ,求直线
,求直线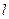 的方程.
的方程.(1)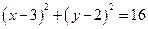 (2)
(2)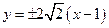 .
.
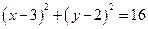 (2)
(2)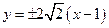 .
.(1)解: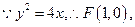 又
又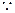 直线
直线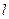 的斜率为1,
的斜率为1,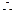 直线
直线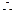
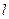 的方程为:
的方程为: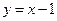 ,代入
,代入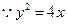 ,得:
,得: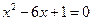 ,由根与系数的关系得:
,由根与系数的关系得: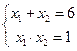 ,易得
,易得 中点即圆心的坐标为
中点即圆心的坐标为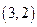 ,又
,又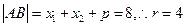 ,
,
 所求的圆的方程为:
所求的圆的方程为: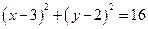 .^
.^
(2)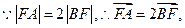 而
而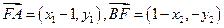 ,
,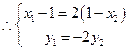 ,
, 直线
直线 的斜率存在,设直线
的斜率存在,设直线 的斜率为
的斜率为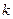 ,则直线
,则直线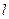 的方程为:
的方程为:
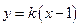 ,代入
,代入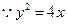 ,得:
,得: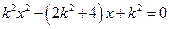 ,由根与系数的关系得:
,由根与系数的关系得:
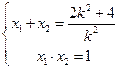 ,
,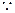
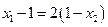 ,
,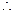
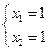 或
或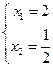 ,
,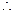
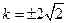 ,
,
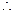 直线
直线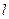 的方程为:
的方程为: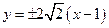 .
.
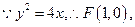 又
又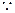 直线
直线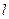 的斜率为1,
的斜率为1,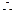 直线
直线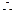
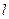 的方程为:
的方程为: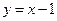 ,代入
,代入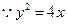 ,得:
,得: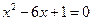 ,由根与系数的关系得:
,由根与系数的关系得: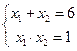 ,易得
,易得 中点即圆心的坐标为
中点即圆心的坐标为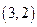 ,又
,又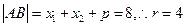 ,
, 所求的圆的方程为:
所求的圆的方程为: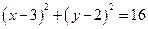 .^
.^(2)
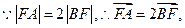 而
而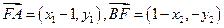 ,
,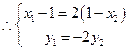 ,
,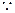 直线
直线 的斜率存在,设直线
的斜率存在,设直线 的斜率为
的斜率为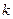 ,则直线
,则直线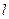 的方程为:
的方程为: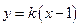 ,代入
,代入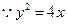 ,得:
,得: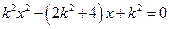 ,由根与系数的关系得:
,由根与系数的关系得: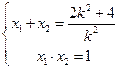 ,
,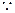
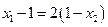 ,
,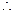
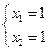 或
或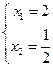 ,
,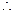
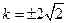 ,
,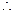 直线
直线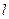 的方程为:
的方程为: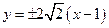 .
.
练习册系列答案
相关题目
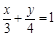 与两坐标轴围成的三角形的周长为( )
与两坐标轴围成的三角形的周长为( )



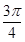 ,直线l1经过点A(3,2)和B(a,-1),且直线l1与直线l垂直,直线l2的方程为2x+by+1=0,且直线l2与直线l1平行,则a+b等于( )
,直线l1经过点A(3,2)和B(a,-1),且直线l1与直线l垂直,直线l2的方程为2x+by+1=0,且直线l2与直线l1平行,则a+b等于( )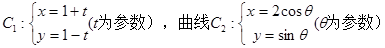 ,若
,若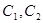 交于A、B两点,则弦长
交于A、B两点,则弦长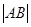 为( )
为( )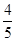 B.
B.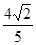 C.
C.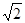 D.4
D.4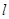 :(2m+1)x+(m+1)y﹣7m﹣4=0恒过一定点P,则点P的坐标为 .
:(2m+1)x+(m+1)y﹣7m﹣4=0恒过一定点P,则点P的坐标为 .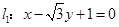 ,
,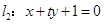 ,若直线
,若直线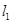 与
与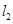 的夹角为
的夹角为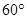 ,则
,则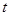 = .
= .