题目内容
12.对于$f(x)={cos^2}({x-\frac{π}{12}})+{sin^2}({x+\frac{5π}{12}})-1$,下列选项中正确的是( )| A. | f(x)关于直线$x=\frac{π}{3}$对称 | B. | f(x)是偶函数 | ||
| C. | f(x)的最小正周期为2π | D. | f(x)的最大值为1 |
分析 利用三角恒等变换化简函数的解析式,再利用余弦函数的图象和性质,逐一判断各个选项是否正确,从而得出结论.
解答 解:对于$f(x)={cos^2}({x-\frac{π}{12}})+{sin^2}({x+\frac{5π}{12}})-1$=$\frac{1+cos(2x-\frac{π}{6})}{2}$+$\frac{1-os(2x+\frac{5π}{6})}{2}$-1=$\frac{1}{2}$cos(2x-$\frac{π}{6}$)-$\frac{1}{2}$cos(2x+$\frac{5π}{6}$)
=$\frac{1}{2}$cos(2x-$\frac{π}{6}$)+$\frac{1}{2}$cos(2x-$\frac{π}{6}$)=cos(2x-$\frac{π}{6}$),
令x=$\frac{π}{3}$,求得f(x)=0,不是最值,故f(x)的图象不关于直线$x=\frac{π}{3}$对称,故A不正确.
由于不满足f(-x)=f(x),故函数不是偶函数,故B不正确.
函数的最小正周期为$\frac{2π}{2}$=π,故C不正确.
函数的最大值为1,故D正确,
故选:D.
点评 本题主要考查三角恒等变换,余弦函数的图象和性质,属于基础题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
7.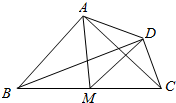 如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
 如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )| A. | 1 | B. | -1 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
17.若数列{an}满足:a1=$\frac{3}{2}$,an=$\frac{1}{2}-\frac{2}{{2{a_{n-1}}+1}}$(n=2,3,4,…),且有一个形如an=Asin(ωn+φ)的通项公式,其中A,ω,φ均为实数,且ω>0,则此通项公式an可以为( )
| A. | an=$\frac{3}{2}sin({\frac{2π}{3}n-\frac{π}{6}})$ | B. | an=$\sqrt{3}sin({\frac{2π}{3}n+\frac{2π}{3}})$ | ||
| C. | an=-$\frac{3}{2}sin({\frac{2π}{3}n+\frac{5π}{6}})$ | D. | an=$\sqrt{3}sin({\frac{2π}{3}n-\frac{π}{3}})$ |
4.设复数z的共轭复数是$\overline{z}$,z=3+i,则$\frac{1}{\overline{z}}$等于( )
| A. | 3+i | B. | 3-i | C. | $\frac{3}{10}$i+$\frac{1}{10}$ | D. | $\frac{3}{10}$+$\frac{1}{10}$i |