题目内容
所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数.
如: ;
; ;
; .
.
已经证明:若 是质数,则
是质数,则 是完全数,
是完全数,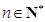 .请写出一个四位完全数 ;又
.请写出一个四位完全数 ;又 ,所以
,所以 的所有正约数之和可表示为
的所有正约数之和可表示为 ;
; ,所以
,所以 的所有正约数之和可表示为
的所有正约数之和可表示为 ;
;
按此规律, 的所有正约数之和可表示为 .
的所有正约数之和可表示为 .
 ;
;
解析试题分析:(1)由若 是质数,则
是质数,则 是完全数可知,
是完全数可知, 是质数,所以
是质数,所以 是完全数。(2)因为
是完全数。(2)因为 ,所以
,所以 的所有正约数之和可表示为
的所有正约数之和可表示为
考点:合情推理。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 >
> ”时,假设的内容应为______________.
”时,假设的内容应为______________.
 ,计算
,计算 ,推测当
,推测当 时,有_____________.
时,有_____________. 与它的高
与它的高 的关系是:
的关系是: ,把这个结论推广到空间正四面体,则正四面体内切球的半径
,把这个结论推广到空间正四面体,则正四面体内切球的半径
 +
+ +…+
+…+ (n∈N*),用数学归纳法证明f(2n)>
(n∈N*),用数学归纳法证明f(2n)> 时,f(2k+1)-f(2k)等于 .
时,f(2k+1)-f(2k)等于 . =2cos
=2cos ,
,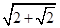 =2cos
=2cos ,
, =2cos
=2cos ,…,请从中归纳出第n个等式:=________.
,…,请从中归纳出第n个等式:=________.