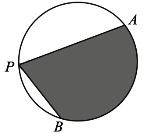
题目内容
【题目】已知三棱锥![]() 中,
中,![]() ,且
,且![]() 、
、![]() 、
、![]() 两两垂直,
两两垂直,![]() 是三棱锥
是三棱锥![]() 外接球面上一动点,则
外接球面上一动点,则![]() 到平面
到平面![]() 的距离的最大值是( )
的距离的最大值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
![]() 是棱长为1的正方体
是棱长为1的正方体![]() 上具有公共顶点
上具有公共顶点![]() 的三条棱,以
的三条棱,以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,三棱锥
轴,建立空间直角坐标系,三棱锥![]() 外接球就是正方体
外接球就是正方体![]() 的外接球,由正方体及球的几何性质可得点
的外接球,由正方体及球的几何性质可得点![]() 与
与![]() 重合时,点
重合时,点![]() 到平面
到平面![]() 的距离最大,求出平面
的距离最大,求出平面![]() 的法向量,由点到直线的距离公式即可得结果.
的法向量,由点到直线的距离公式即可得结果.
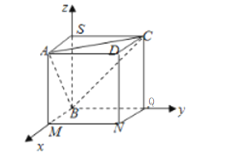
![]() 三棱锥
三棱锥![]() ,满足
,满足![]() 两两垂直,且
两两垂直,且![]() ,
,
![]() 如图
如图![]() 是棱长为1的正方体
是棱长为1的正方体![]() 上具有公共顶点
上具有公共顶点![]() 的三条棱,
的三条棱,
以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
,
![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则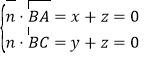 ,取
,取![]() ,得
,得![]() ,
,
三棱锥![]() 外接球就是棱长为1的正方体
外接球就是棱长为1的正方体![]() 的外接球,
的外接球,
![]() 是三棱锥
是三棱锥![]() 外接球上一动点,
外接球上一动点,
![]() 由正方体与球的几何性质可得,点
由正方体与球的几何性质可得,点![]() 点与
点与![]() 重合时,
重合时,
点![]() 到平面
到平面![]() 的距离最大,
的距离最大,
![]() 点
点![]() 到平面
到平面![]() 的距离的最大值为
的距离的最大值为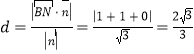 .故选C.
.故选C.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案【题目】每年的金秋十月,越野e族阿拉善英雄会在内蒙古自治区阿拉善盟阿左旗腾格里沙漠举行,该项目已打造成集沙漠竞技运动、汽车文化极致体验、主题休闲度假为一体的超级汽车文化赛事娱乐综合体.为了减少对环境的污染,某环保部门租用了特制环保车清洁现场垃圾.通过查阅近5年英雄会参会人数![]() (万人)与沙漠中所需环保车辆数量
(万人)与沙漠中所需环保车辆数量![]() (辆),得到如下统计表:
(辆),得到如下统计表:
参会人数 | 11 | 9 | 8 | 10 | 12 |
所需环保车辆 | 28 | 23 | 20 | 25 | 29 |
(1)根据统计表所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知租用的环保车平均每辆的费用![]() (元)与数量
(元)与数量![]() (辆)的关系为
(辆)的关系为
![]() .主办方根据实际参会人数为所需要投入使用的环保车,
.主办方根据实际参会人数为所需要投入使用的环保车,
每辆支付费用6000元,超出实际需要的车辆,主办方不支付任何费用.预计本次英雄会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测环保部门在确保清洁任务完成的前提下,应租用多少辆环保车?获得的利润![]() 是多少?(注:利润
是多少?(注:利润![]() 主办方支付费用
主办方支付费用![]() 租用车辆的费用).
租用车辆的费用).
参考公式:
【题目】对某城市居民家庭年收入![]() (万元)和年“享受资料消费”
(万元)和年“享受资料消费”![]() (万元)进行统计分析,得数据如表所示.
(万元)进行统计分析,得数据如表所示.
| 6 | 8 | 10 | 12 |
| 2 | 3 | 5 | 6 |
(1)请根据表中提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)若某家庭年收入为18万元,预测该家庭年“享受资料消费”为多少?
(参考公式: ,
,![]() )
)