题目内容
16.向量 $\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=4,|$\overrightarrow{a}$+$\overrightarrow{b}$|=5,则|$\overrightarrow{a}$-$\overrightarrow{b}$|=5.分析 运用向量的平方即为模的平方,可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,再由向量的平方即为模的平方,可得|$\overrightarrow{a}$-$\overrightarrow{b}$|=5.
解答 解:向量 $\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=4,|$\overrightarrow{a}$+$\overrightarrow{b}$|=5,
可得|$\overrightarrow{a}$+$\overrightarrow{b}$|2=$\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=25,
即有9+2$\overrightarrow{a}$•$\overrightarrow{b}$+16=25,
即为$\overrightarrow{a}$•$\overrightarrow{b}$=0,
则|$\overrightarrow{a}$-$\overrightarrow{b}$|2=$\overrightarrow{a}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=25,
即为|$\overrightarrow{a}$-$\overrightarrow{b}$|=5.
故答案为:5.
点评 本题考查向量的数量积的性质,考查向量的平方即为模的平方,考查运算能力,属于基础题.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案(1)求数列{an},{bn}的通项公式.
(2)设cn=an•bn,求数列{cn}的前n项和Tn.
| A. | 8 | B. | 10 | C. | 9或10 | D. | 8和9 |
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
 中,
中,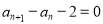 ,且
,且 ,则
,则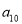 等于( )
等于( )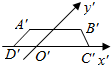 (1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.
(1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.