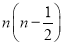题目内容
5.设等差数列{an}的公差为d,则a1d>0是数列{${3}^{{a}_{1}{a}_{n}}$}为递增数列的( )| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
分析 根据充分必要条件的定义结合数列以及复合函数的单调性判断即可.
解答 解:∵数列{an}是公差为d的等差数列,
若数列{${3}^{{a}_{1}{a}_{n}}$}即数列{a1an}为递增数列,
则a1an-a1an-1=a1(an-an-1)=a1d>0,
是必要条件;
若a1d>0,则数列{a1an}是递增数列即数列{${3}^{{a}_{1}{a}_{n}}$}为递增数列,
是充分条件,
故选:A.
点评 本题考查了充分必要条件,考查数列的性质以及复合函数的单调性问题,是一道基础题.

练习册系列答案
相关题目
9.已知二次函数y=x2+ax+1与x轴的正半轴有两个不同的交点,则实数a的取值范围是( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2) | C. | (2,+∞) | D. | (-∞,0) |
 是圆
是圆 的直径,点
的直径,点 是圆
是圆 的点,
的点, 垂直于圆
垂直于圆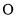 所在的平面,且
所在的平面,且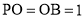 .
.
 为线段
为线段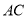 的中点,求证
的中点,求证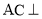 平面
平面 ;
; 体积的最大值;
体积的最大值;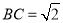 ,点
,点 在线段
在线段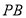 上,求
上,求 的最小值.
的最小值. ,且
,且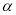 为第四象限角,则
为第四象限角,则 的值等于
的值等于 B.
B. C.
C.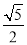 D.
D.
 B.
B.
 D.
D.