题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{2x-{x}^{2},0≤x≤1}\\{-{x}^{2},-1≤x<0}\end{array}\right.$,则函数f(x)的图象与直线y=x围成的封闭图形的面积为$\frac{1}{3}$.分析 首先画出函数图象,找出函数f(x)的图象与直线y=x围成的封闭图形,利用定积分表示出其面积,然后计算即可.
解答 解:由题意,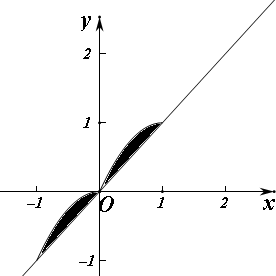 函数f(x)的图象与直线y=x围成的封闭图形如图阴影部分,
函数f(x)的图象与直线y=x围成的封闭图形如图阴影部分,
曲线y=2x-x2与直线y=x的交点坐标为(0,0),(1,1)
∴曲线y=-x2与直线y=x的交点为(0,0),(-1,-1),
所以函数f(x)的图象与直线y=x围成的封闭图形的面积为S=${∫}_{-1}^{0}(-{x}^{2}-x)dx+{∫}_{0}^{1}(2x-{x}^{2}-x)dx$=(-$\frac{1}{3}{x}^{3}-\frac{1}{2}{x}^{2}$)|${\;}_{-1}^{0}$+($\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}$)|${\;}_{0}^{1}$=$\frac{1}{3}$;
故答案为:$\frac{1}{3}$.
点评 本题考查定积分知识的运用,关键是画出图形,利用定积分表示封闭图形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.定义在R上的函数f(x)是周期为π的函数,当-$\frac{π}{2}$≤x<$\frac{π}{2}$时,f(x)=1-cosx,若方程f(x)-kx=0至少有5个根,则k的取值范围是( )
| A. | [0,$\frac{2}{3π}$) | B. | [0,$\frac{2}{3π}$] | C. | (-$\frac{2}{3π}$,$\frac{2}{3π}$) | D. | [-$\frac{2}{3π}$,$\frac{2}{3π}$] |
17.已知sinθ=$\frac{3}{5}$,$\frac{5π}{2}$<θ<3π,那么tan$\frac{θ}{2}$+cos$\frac{θ}{2}$的值为( )
| A. | $\frac{\sqrt{10}}{10}$-3 | B. | 3-$\frac{\sqrt{10}}{10}$ | C. | -3-$\frac{\sqrt{10}}{10}$ | D. | 3+$\frac{\sqrt{10}}{10}$ |