题目内容
【题目】为了研究某种细菌随时间x变化,繁殖的个数,收集数据如下:
![]()
(1)用天数作解释变量,繁殖个数作预报变量,作出这些数据的散点图,根据散点图判断:![]() 与y=
与y=![]() 哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)
哪一个作为繁殖的个数y关于时间x变化的回归方程类型为最佳?(给出判断即可,不必说明理由)
|
|
|
|
|
|
3.5 | 62.83 | 3.53 | 17.5 | 596.505 | 12.04 |
其中![]() ;
;![]()
(2)根据(1)的判断最佳结果及表中的数据,建立y关于x 的回归方程。
参考公式: 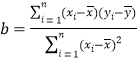
![]()
【答案】(1)选择y=![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)根据收集数据,可得数据的散点图,由散点图看出样本点分布在一条指数函数y=![]() 的周围,于是选择y=
的周围,于是选择y=![]() ;
;
(2)由散点图看出样本点分布在一条指数型曲线y=cebx(c>0)的周围,则lny=bx+lnc.变换后的样本点分布在一条直线附近,因此可以用线性回归方程来拟合,即可求出y对x的回归方程.
详解:(1)由散点图看出样本点分布在一条指数函数y=![]() 的周围,于是选择y=
的周围,于是选择y=![]()
作出散点图如图1所示.
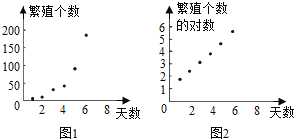
(2)令Z=lny,则![]()
x | 1 | 2 | 3 | 4 | 5 | 6 |
Z | 1.79 | 2.48 | 3.22 | 3.89 | 4.55 | 5.25 |
由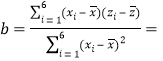
![]() ,
,![]() 1.122
1.122
得y=![]()
![]() ; 则有
; 则有![]()

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案【题目】如图,正三棱柱ABC-A1B1C1中,D是AC中点,且直线AB1与平面BCC1B1所成的角为300,则异面直线AB1与BD所成角的大小为 ( )

A. 300
B. 450
C. 600
D. 900
【题目】一只药用昆虫的产卵数![]() 与一定范围内的温度
与一定范围内的温度![]() 有关,现收集了该种药用昆虫的6组观测数据如下表:
有关,现收集了该种药用昆虫的6组观测数据如下表:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数 | 6 | 11 | 20 | 27 | 57 | 77 |
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求![]() 关
关![]() 的回归方程为
的回归方程为![]() ,且相关指数
,且相关指数![]()
①试与(1)中的线性回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
②用拟合效果好的模型预测温度为![]() 时该种药用昆虫的产卵数(结果取整数).
时该种药用昆虫的产卵数(结果取整数).
附:一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为 ;相关指数
;相关指数 .
.