题目内容
(本题满分16分)
2010年上海世博会某国要建一座八边形(不一定为正八边形)的展馆区(如图),它的主体造型的平面图是由二个相同的矩形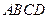 和
和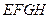 构成的面积为
构成的面积为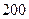 m2的十字型地域,计划在正方形
m2的十字型地域,计划在正方形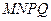 上建一座“观景花坛”,造价为
上建一座“观景花坛”,造价为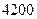 元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为
元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为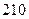 元/m2,再在四个空角(如
元/m2,再在四个空角(如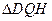 等)上铺草坪,造价为
等)上铺草坪,造价为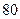 元/m2. 设总造价为
元/m2. 设总造价为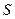 元,
元,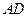 长为
长为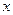 m.
m.
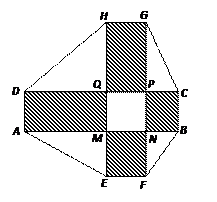 (1)用
(1)用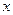 表示矩形
表示矩形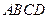 的边
的边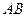 的长
的长
(1)试建立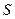 与
与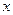 的函数关系
的函数关系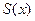
(2)当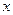 为何值时,
为何值时,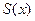 最小?并求这个最小值
最小?并求这个最小值
2010年上海世博会某国要建一座八边形(不一定为正八边形)的展馆区(如图),它的主体造型的平面图是由二个相同的矩形
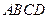 和
和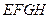 构成的面积为
构成的面积为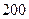 m2的十字型地域,计划在正方形
m2的十字型地域,计划在正方形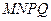 上建一座“观景花坛”,造价为
上建一座“观景花坛”,造价为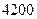 元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为
元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为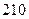 元/m2,再在四个空角(如
元/m2,再在四个空角(如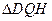 等)上铺草坪,造价为
等)上铺草坪,造价为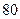 元/m2. 设总造价为
元/m2. 设总造价为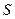 元,
元,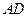 长为
长为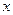 m.
m.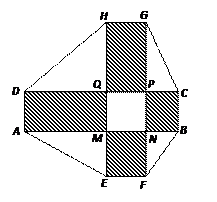 (1)用
(1)用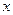 表示矩形
表示矩形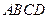 的边
的边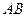 的长
的长(1)试建立
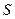 与
与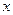 的函数关系
的函数关系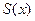
(2)当
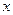 为何值时,
为何值时,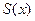 最小?并求这个最小值
最小?并求这个最小值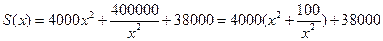
当
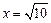 米时,
米时,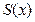 有最小值为
有最小值为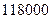 元
元1)由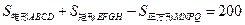 得:
得:
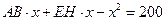
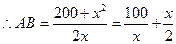 . ……………………..3分
. ……………………..3分
(2)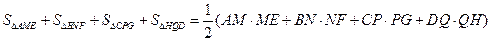
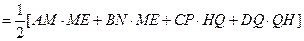
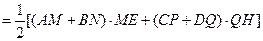
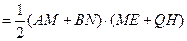
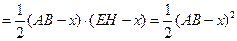
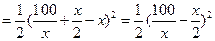 ……………………..7分
……………………..7分
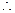
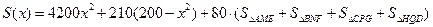
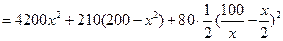
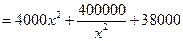
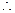
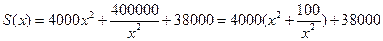 .…..11分
.…..11分
(3)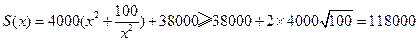 ………..13分
………..13分
当且仅当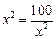 ,即
,即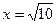 时,
时,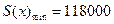 . ………..15分
. ………..15分
所以当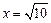 米时,
米时,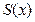 有最小值为
有最小值为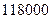 元. ……………………..16分
元. ……………………..16分
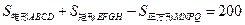 得:
得: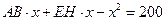
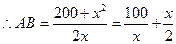 . ……………………..3分
. ……………………..3分(2)
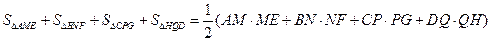
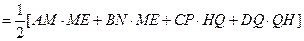
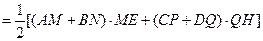
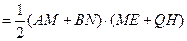
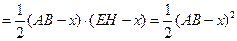
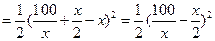 ……………………..7分
……………………..7分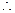
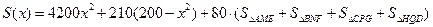
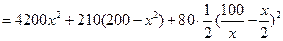
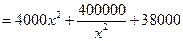
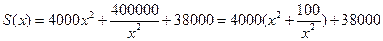 .…..11分
.…..11分(3)
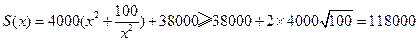 ………..13分
………..13分当且仅当
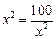 ,即
,即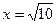 时,
时,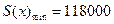 . ………..15分
. ………..15分所以当
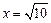 米时,
米时,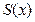 有最小值为
有最小值为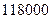 元. ……………………..16分
元. ……………………..16分
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
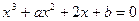 有三个实数根,它们分别可作为抛物线、双曲线、椭圆的离心率,则实数a的取值范围是 ▲ .
有三个实数根,它们分别可作为抛物线、双曲线、椭圆的离心率,则实数a的取值范围是 ▲ .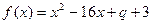 。
。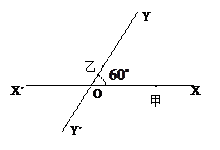
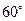 的直路
的直路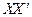 ,
,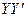 ,交点是
,交点是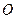 ,甲、乙分别在
,甲、乙分别在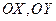 上,起初甲离O点3 km,乙离O点1 km,后甲沿
上,起初甲离O点3 km,乙离O点1 km,后甲沿 方向用4km/h的速度同时步行. 设t小时后甲在
方向用4km/h的速度同时步行. 设t小时后甲在 的奇函数的为
的奇函数的为
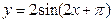
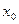 是方程式
是方程式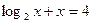 的解,则
的解,则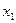 、
、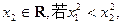 则
则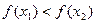 ,现给定函数①
,现给定函数①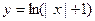 ②
② ③
③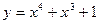
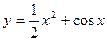
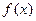 与
与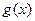 表示同一函数的一组是 ( )
表示同一函数的一组是 ( )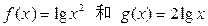
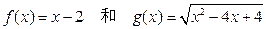
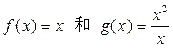
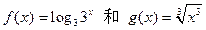
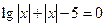 在区间
在区间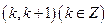 上有零点,则所有满足条件的
上有零点,则所有满足条件的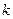 的值的和为 ______.
的值的和为 ______.