题目内容
（2013•汕头一模）设α、β为两个不同的平面，m、n为两条不同的直线，且m?α，n?β，有两命题：p：若m∥n，则α∥β；q：若m⊥β，则α⊥β；那么（ ）
分析：根据平面和平面平行的判定定理得出p为假命题，根据平面和平面垂直的判定定理，q是真命题．再利用符合命题真假的判断，逐项考察各选项．
解答：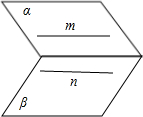
解：p：若m∥n，则α∥β，此命题为假命题．如图所示
α与β相交．p是假命题．
q：若m⊥β，则α⊥β；根据平面和平面垂直的判定定理，此命题为真命题．
所以：p或q”是真命题，A错
“p且q”是假命题，B错．
“非p或q”是真命题，C错．
非p且q”是真命题，D对．
故选D．
解：p：若m∥n，则α∥β，此命题为假命题．如图所示α与β相交．p是假命题．
q：若m⊥β，则α⊥β；根据平面和平面垂直的判定定理，此命题为真命题．
所以：p或q”是真命题，A错
“p且q”是假命题，B错．
“非p或q”是真命题，C错．
非p且q”是真命题，D对．
故选D．
点评：本题以直线、平面之间位置关系为出发，考查符合命题真假的判断．属于基础题．
练习册系列答案
发散思维新课堂系列答案
相关题目