题目内容
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:平面内到两个定点![]() 的距离之比为定值
的距离之比为定值![]() 的点所形成的图形是圆.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系
的点所形成的图形是圆.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,点
,点![]() 满足
满足![]() .设点
.设点![]() 所构成的曲线为
所构成的曲线为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.![]() 的方程为
的方程为![]()
B.在![]() 上存在点
上存在点![]() ,使得
,使得![]() 到点
到点![]() 的距离为
的距离为![]()
C.在![]() 上存在点
上存在点![]() ,使得
,使得![]()
D.在![]() 上存在点
上存在点![]() ,使得
,使得![]()
【答案】BD
【解析】
通过设出点P的坐标,利用![]() ,即可求出曲线
,即可求出曲线![]() 的轨迹方程,然后假设曲线
的轨迹方程,然后假设曲线![]() 上一点坐标,根据BCD选项逐一列出所满足条件,然后与
上一点坐标,根据BCD选项逐一列出所满足条件,然后与![]() 的轨迹方程联立,判断是否有解,即可得出答案.
的轨迹方程联立,判断是否有解,即可得出答案.
设点![]() ,由
,由![]() ,
,
得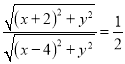 ,化简得
,化简得![]() ,即
,即![]() ,故A选项错误;
,故A选项错误;
对于B选项,设![]() ,由
,由![]() 到点
到点![]() 的距离为
的距离为![]() ,得
,得![]() ,又
,又![]() ,联立方程可知有解,故B选项正确;
,联立方程可知有解,故B选项正确;
对于C选项,设![]() ,由
,由![]() ,得
,得![]() ,又
,又![]() ,联立方程可知无解,故C选项错误;
,联立方程可知无解,故C选项错误;
对于D选项,设![]() ,由
,由![]() ,得
,得![]() ,又
,又![]() ,联立方程可知有解,故D选项正确.
,联立方程可知有解,故D选项正确.
故选:BD

练习册系列答案
相关题目