题目内容
9.已知向量$\overrightarrow m=(2,-1)$,$\overrightarrow n=(sin\frac{A}{2},cos(B+C))$,A,B,C为△ABC的内角,其对应边应为a,b,c.(1)若A=120°,求$|\overrightarrow n|$的值;
(2)当$\overrightarrow m•\overrightarrow n$取得最大值时,求角A的大小;
(3)在(2)成立的条件下,当$a=\sqrt{3}$时,求b2+c2的取值范围.
分析 (1)由A=120°,可得B+C=60°,利用数量积运算性质即可得出$|\overrightarrow n|$;
(2)$\overrightarrow m•\overrightarrow n$=-2$(sin\frac{A}{2}-\frac{1}{2})^{2}$+$\frac{3}{2}$,利用二次函数与三角函数的值域即可得出.
(3)由余弦定理可得:a2=b2+c2-2bccosA,利用基本不等式可得:b2+c2=3+$\sqrt{3}$bc≤3+$\sqrt{3}$×$\frac{{b}^{2}+{c}^{2}}{2}$,即可得出.
解答 解:(1)∵A=120°,∴B+C=60°,
∴$|\overrightarrow n|$=$\sqrt{si{n}^{2}6{0}^{°}+co{s}^{2}6{0}^{°}}$=1;
(2)$\overrightarrow m•\overrightarrow n$=$2sin\frac{A}{2}$-cos(B+C)
=cosA+2$sin\frac{A}{2}$
=$1-2si{n}^{2}\frac{A}{2}$+2sin$\frac{A}{2}$
=-2$(sin\frac{A}{2}-\frac{1}{2})^{2}$+$\frac{3}{2}$,
当$sin\frac{A}{2}$=$\frac{1}{2}$,∵A∈(0°,180°),A=30°时,$\overrightarrow m•\overrightarrow n$取得最大值.
(3)由余弦定理可得:a2=b2+c2-2bccosA,
∴b2+c2=3+$\sqrt{3}$bc≤3+$\sqrt{3}$×$\frac{{b}^{2}+{c}^{2}}{2}$,
化为b2+c2≤$\frac{6}{2-\sqrt{3}}$=$12+6\sqrt{3}$,当且仅当b=c=6+3$\sqrt{3}$.
∴b2+c2的取值范围是$(0,12+6\sqrt{3}]$.
点评 本题考查了向量数量积运算性质、余弦定理、基本不等式的性质、三角函数的单调性、同角三角函数的基本关系式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | z | 400 |
| 标准型 | 300 | 450 | 600 |
(1)求z的值;
(2)用分层抽样的方法在B类轿车中抽取一个容量为8的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率.
| A. | 4 | B. | $\sqrt{10}$ | C. | 2$\sqrt{5}$ | D. | 1 |
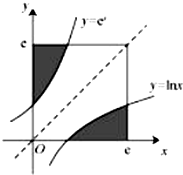
| A. | 2 | B. | $\frac{2}{e}$ | C. | e2 | D. | e |
| A. | 16 | B. | -16 | C. | 8 | D. | -8 |
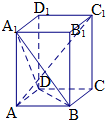 在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,给出下列结论:
在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,给出下列结论: