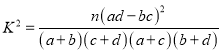题目内容
【题目】给出下列五个命题:
①函数y= ![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②若lna<1成立,则a的取值范围是(﹣∞,e);
③函数f(x)=ax+1﹣2(a>0,a≠1)的图象过定点(﹣1,﹣1);
④方程x2+(a﹣3)x+a=0的有一个正实根,一个负实根,则a<0;
⑤函数f(x)=loga(6﹣ax)(a>0,a≠1)在[0,2]上为减函数,则1<a<3.
其中正确的个数( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:①函数y= ![]() =0(x=±1),既是偶函数,又是奇函数,故①错误;
=0(x=±1),既是偶函数,又是奇函数,故①错误;
②若lna<1成立,则a的取值范围是(0,e),故②错误;
③∵y=ax的图象恒过(0,1),∴函数f(x)=ax+1﹣2(a>0,a≠1)的图象过定点(﹣1,﹣1),故③正确;
④方程x2+(a﹣3)x+a=0有一个正实根,一个负实根,则 ![]() ,即a<0,故④正确;
,即a<0,故④正确;
⑤∵a>0,a≠1,∴内函数t=6﹣ax为定义域上的减函数,要使函数f(x)=loga(6﹣ax)(a>0,a≠1)在[0,2]上为减函数,
则 ![]() ,即1<a<3,故⑤正确.
,即1<a<3,故⑤正确.
∴正确的命题个数是3个.
故选:C.
【考点精析】通过灵活运用命题的真假判断与应用,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系即可以解答此题.

【题目】某校高一年级共有1000名学生,其中男生400名,女生600名,该校组织了一次口语模拟考试(满分为100分).为研究这次口语考试成绩为高分(80分以上(含80分)为高分)是否与性别有关,现按性别采用分层抽样的方法抽取100名学生的成绩,按从低到高分成![]() 七组,并绘制成如图所示的频率分布直方图.已知区间
七组,并绘制成如图所示的频率分布直方图.已知区间![]() 上的频率等于区间
上的频率等于区间![]() 上频率,区间
上频率,区间![]() 上的频率与区间
上的频率与区间![]() 上的频率之比为
上的频率之比为![]() .
.
| 0.010 | 0.050 | 0.025 | 0.010 | 0.001 |
| 6.635 | 3.841 | 5.024 | 6.635 | 10.828 |
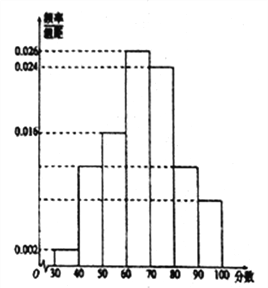
(1)估计该校高一年级学生在口语考试中,成绩为高分的人数;
(2)请你根据已知条件将下列![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“该校高一年级学生在本次考试中口语成绩及格(60分以上(含60分)为及格)与性别有关”.
的把握认为“该校高一年级学生在本次考试中口语成绩及格(60分以上(含60分)为及格)与性别有关”.
 附:
附: