题目内容
【题目】已知f(x)为偶函数,当x≥0时,f(x)=﹣(x﹣1)2+1,则满足f[f(a)+ ![]() ]=
]= ![]() 的实数a的个数为( )
的实数a的个数为( )
A.2
B.4
C.6
D.8
【答案】C
【解析】解:设t=f(a)+ ![]() ,
,
则条件等价为f(t)= ![]() ,
,
若x≤0,则﹣x≥0,
∵当x≥0时,f(x)=﹣(x﹣1)2+1,
∴当﹣x≥0时,f(﹣x)=﹣(﹣x﹣1)2+1=﹣(x+1)2+1,
∵f(x)为偶函数,
∴f(﹣x)=﹣(x+1)2+1=f(x),
即f(x)=﹣(x+1)2+1,x≤0,
作出函数f(x)的图象如图:
当x≥0时,由﹣(x﹣1)2+1= ![]() ,得(x﹣1)2=
,得(x﹣1)2= ![]() ,则x=1+
,则x=1+ ![]() 或x=1﹣
或x=1﹣ ![]() ,
,
∵f(x)为偶函数,
∴当x<0时,f(x)= ![]() 的解为x3=﹣1﹣
的解为x3=﹣1﹣ ![]() ,x4=﹣1+
,x4=﹣1+ ![]() ;
;
综上所述,f(t)= ![]() 得解为t1=1+
得解为t1=1+ ![]() 或t2=1﹣
或t2=1﹣ ![]() ,t3=﹣1﹣
,t3=﹣1﹣ ![]() ,t4=﹣1+
,t4=﹣1+ ![]() ;
;
由t=f(a)+ ![]() 得,
得,
若t1=1+ ![]() ,则f(a)+
,则f(a)+ ![]() =1+
=1+ ![]() ,即f(a)=
,即f(a)= ![]() +
+ ![]() >1,此时a无解,
>1,此时a无解,
若t2=1﹣ ![]() ,则f(a)+
,则f(a)+ ![]() =1﹣
=1﹣ ![]() ,即f(a)=﹣
,即f(a)=﹣ ![]() ﹣
﹣ ![]() ∈(﹣∞,0),此时a有2个解,
∈(﹣∞,0),此时a有2个解,
若t3=﹣1﹣ ![]() ,则f(a)+
,则f(a)+ ![]() =﹣1﹣
=﹣1﹣ ![]() ,即f(a)=﹣
,即f(a)=﹣ ![]() ﹣
﹣ ![]() ∈(﹣∞,0),此时a有2个解,
∈(﹣∞,0),此时a有2个解,
若t4=﹣1+ ![]() ,则f(a)+
,则f(a)+ ![]() =﹣1+
=﹣1+ ![]() ,即f(a)=﹣
,即f(a)=﹣ ![]() +
+ ![]() ∈(﹣∞,0),此时a有2个解,
∈(﹣∞,0),此时a有2个解,
故共有2+2+2=6个解.
故选:C.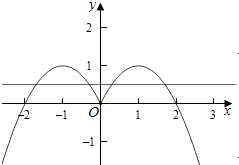
利用换元法将函方程转化为f(t)= ![]() ,利用数形结合进行求解即可.
,利用数形结合进行求解即可.

练习册系列答案
相关题目