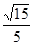题目内容
若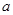 、
、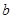 是直线,
是直线,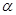 、
、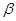 是平面,
是平面,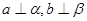 ,向量
,向量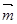 在
在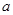 上,向量
上,向量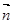 在
在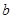 上,
上,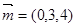 ,
,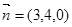 ,则
,则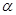 、
、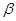 所成二面角中较小的一个余弦值为 .
所成二面角中较小的一个余弦值为 .
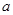 、
、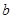 是直线,
是直线,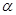 、
、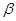 是平面,
是平面,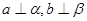 ,向量
,向量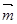 在
在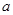 上,向量
上,向量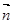 在
在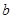 上,
上,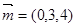 ,
,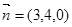 ,则
,则 、
、 所成二面角中较小的一个余弦值为 .
所成二面角中较小的一个余弦值为 .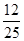
试题分析:根据题意可知,由于
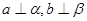 ,且有向量
,且有向量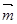 在
在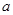 上,向量
上,向量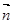 在
在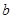 上,如果
上,如果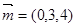 ,
,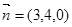 ,那么结合向量数量积公式可知,
,那么结合向量数量积公式可知,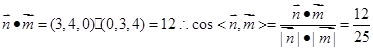 ,故答案为
,故答案为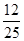
点评:解决的管家式利用平面法向量以及二面角的求解的方法可知结论,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
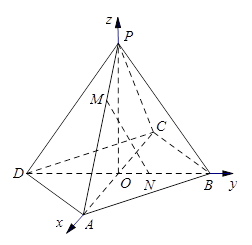
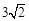 ,点M,N分别在PA,BD上,且
,点M,N分别在PA,BD上,且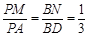 .
.
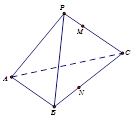
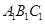 中,D,E分别是AB,BB1的中点,
中,D,E分别是AB,BB1的中点,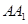 =AC=CB=
=AC=CB=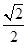 AB.
AB.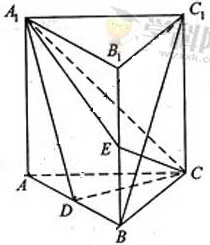
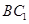 //平面
//平面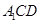 ;
;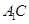 -E的正弦值.
-E的正弦值.



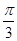 ,π);
,π);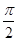 ;
;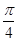 的直线有3条;
的直线有3条;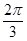 ,则过点N与平面PAC和平面PAB都成
,则过点N与平面PAC和平面PAB都成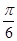 的直线有3条.
的直线有3条. 中
中 与截面
与截面 所成的角是
所成的角是



 中,
中, =2
=2 ,
, =
= ,则二面角
,则二面角 的大小是 ( )
的大小是 ( )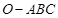 的侧棱
的侧棱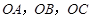 两两垂直,且
两两垂直,且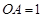 ,
,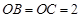 ,
,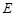 是
是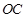 的中点.
的中点.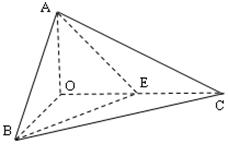
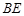 与
与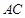 所成角的余弦值;
所成角的余弦值;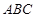 所成角的正弦值.
所成角的正弦值.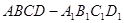 中,AB=BC=2,
中,AB=BC=2,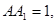 则
则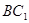 与面
与面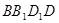 所成角的正弦值为( )
所成角的正弦值为( )