题目内容
正方体 中
中 与截面
与截面 所成的角是
所成的角是
 中
中 与截面
与截面 所成的角是
所成的角是A. | B. | C. | D. |
A
试题分析:连接
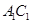 交
交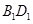 于点
于点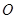 ,连接
,连接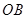 ,则
,则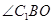 为直线
为直线 与平面
与平面 所成的角,在
所成的角,在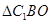 中,
中,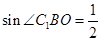 ,所以直线
,所以直线 与平面
与平面 所成的角的大小为
所成的角的大小为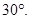
点评:考查直线和平面所成的角,求直线和平面所成的角关键是找到斜线在平面内的射影,把空间角转化为平面角求解,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
 中
中 与截面
与截面 所成的角是
所成的角是A. | B. | C. | D. |
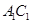 交
交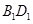 于点
于点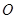 ,连接
,连接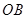 ,则
,则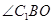 为直线
为直线 与平面
与平面 所成的角,在
所成的角,在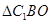 中,
中,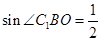 ,所以直线
,所以直线 与平面
与平面 所成的角的大小为
所成的角的大小为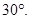

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案