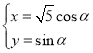题目内容
【题目】设点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() :
:![]()
![]() 的左、右焦点,且椭圆
的左、右焦点,且椭圆![]() 上的点到点
上的点到点![]() 的距离的最小值为
的距离的最小值为![]() .点M、N是椭圆
.点M、N是椭圆![]() 上位于
上位于![]() 轴上方的两点,且向量
轴上方的两点,且向量![]() 与向量
与向量![]() 平行.
平行.
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 时,求△
时,求△![]() 的面积;
的面积;
(3)当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据椭圆的简单性质可得![]() ,解得即可,
,解得即可,
(2)可设![]() ,
,![]() ,根据向量的数量积求出点
,根据向量的数量积求出点![]() 的坐标,再根据直线平行,求出
的坐标,再根据直线平行,求出![]() 的坐标,
的坐标,
利用两点间的距离公式和点到直线的距离公式和三角形的面积公式计算即可,
(3)向量![]() 与向量
与向量![]() 平行,不妨设
平行,不妨设![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,根据坐标之间的关系,求得
,根据坐标之间的关系,求得![]() 的坐标,再根据向量的模,即可求出
的坐标,再根据向量的模,即可求出![]() 的值,根据斜率公式求出直线的斜率,根据直线平行和点斜式即可求出直线方程.
的值,根据斜率公式求出直线的斜率,根据直线平行和点斜式即可求出直线方程.
解:(1)点![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,
![]() ,
,![]() ,
,
![]() 椭圆
椭圆![]() 上的点到点
上的点到点![]() 的距离的最小值为
的距离的最小值为![]() ,
,
![]() ,
,
解得![]() ,
,
![]() 椭圆的方程为
椭圆的方程为![]() ,
,
(2)由(1)可得![]() ,
,![]() ,
,
点![]() 、
、![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的两点,
轴上方的两点,
可设![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,
解得![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() 向量
向量![]() 与向量
与向量![]() 平行,
平行,
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,
![]() 直线方程为
直线方程为![]() ,
,
联立方程组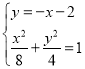 ,解得
,解得![]() ,
,![]() (舍去),或
(舍去),或![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
点![]() 到直线直线
到直线直线![]() 的距离为
的距离为![]() ,
,
![]()
![]() 的面积
的面积![]() ,
,
(3)![]() 向量
向量![]() 与向量
与向量![]() 平行,
平行,
![]() ,
,
![]()
![]() ,
,
![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
解得![]() ,或
,或![]() (舍去)
(舍去)
![]() ,
,
![]() ,
,
![]() ,
,
![]()
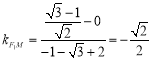 ,
,
![]() 直线
直线![]() 的方程为
的方程为![]() ,
,
即为![]()

练习册系列答案
相关题目