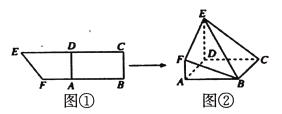
题目内容
【题目】对于数列![]() ,若
,若![]() (
(![]() 是与
是与![]() 无关的常数,
无关的常数,![]() )则称数列
)则称数列![]() 叫做“弱等差数列”已知数列
叫做“弱等差数列”已知数列![]() 满足:
满足:![]() 且
且![]() ,对于
,对于![]() 恒成立,(其中
恒成立,(其中![]() 都是常数)
都是常数)
(1)求证:数列![]() 是“弱等差数列”,并求出数列
是“弱等差数列”,并求出数列![]() 的通项公式
的通项公式
(2)当![]() 时,若数列
时,若数列![]() 是单调递增数列,求
是单调递增数列,求![]() 的取值范围
的取值范围
(3)若![]() ,且
,且![]() ,数列
,数列![]() 满足:
满足:![]() ,求
,求![]()
【答案】(1)证明见解析;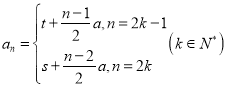 ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() 与已知等式作差可证得
与已知等式作差可证得![]() ,从而证得结论;分别在
,从而证得结论;分别在![]() 和
和![]() 两种情况下利用等差数列通项公式求得通项,从而得到结果;
两种情况下利用等差数列通项公式求得通项,从而得到结果;
(2)由数列的单调性得到![]() ,从而得到恒成立的不等式,解不等式可求得结果;
,从而得到恒成立的不等式,解不等式可求得结果;
(3)采用裂项相消的方式可得到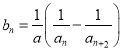 ;由极限的思想可得到
;由极限的思想可得到![]() ,从而整理可得到
,从而整理可得到 ,代入通项公式可求得结果.
,代入通项公式可求得结果.
(1)由![]() 得:
得:![]()
![]()
![]() 为常数
为常数 ![]() 数列
数列![]() 为“弱等差数列”
为“弱等差数列”
当![]() 为奇数时,设
为奇数时,设![]() ,则
,则![]() 成等差数列,公差为
成等差数列,公差为![]()
![]()
当![]() 为偶数时,设
为偶数时,设![]() ,则
,则![]() 成等差数列,公差为
成等差数列,公差为![]()
![]()
综上所述: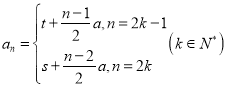
(2)当![]() ,
,![]() 时,
时,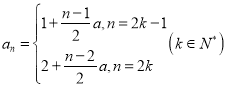
![]() 是单调递增数列
是单调递增数列 ![]()
![]()
由![]() 得:
得:![]() ;由
;由![]() 得:
得:![]()
综上所述:![]() 的取值范围为
的取值范围为![]()
(3)![]()
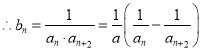
![]()
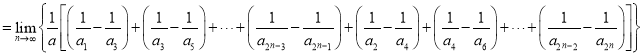
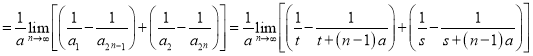
![]()

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
【题目】垃圾分一分,城市美十分;垃圾分类,人人有责.某市为进一步推进生活垃圾分类工作,调动全民参与的积极性,举办了“垃圾分类游戏挑战赛”.据统计,在为期![]() 个月的活动中,共有
个月的活动中,共有![]() 万人次参与.为鼓励市民积极参与活动,市文明办随机抽取
万人次参与.为鼓励市民积极参与活动,市文明办随机抽取![]() 名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
名参与该活动的网友,以他们单次游戏得分作为样本进行分析,由此得到如下频数分布表:
单次游戏得分 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)根据数据,估计参与活动的网友单次游戏得分的平均值及标准差(同一组中的数据用该组区间的中点值作代表);(其中标准差的计算结果要求精确到![]() )
)
(2)若要从单次游戏得分在![]() 、
、![]() 、
、![]() 的三组参与者中,用分层抽样的方法选取
的三组参与者中,用分层抽样的方法选取![]() 人进行电话回访,再从这
人进行电话回访,再从这![]() 人中任选
人中任选![]() 人赠送话费,求此
人赠送话费,求此![]() 人单次游戏得分不在同一组内的概率.
人单次游戏得分不在同一组内的概率.
附:![]() ,
,![]() .
.