题目内容
(2011•湖北)已知向量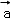 =(x+z,3),
=(x+z,3),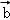 =(2,y﹣z),且
=(2,y﹣z),且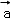 ⊥
⊥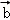 ,若x,y满足不等式|x|+|y|≤1,则z的取值范围为( )
,若x,y满足不等式|x|+|y|≤1,则z的取值范围为( )
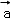 =(x+z,3),
=(x+z,3),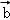 =(2,y﹣z),且
=(2,y﹣z),且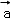 ⊥
⊥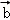 ,若x,y满足不等式|x|+|y|≤1,则z的取值范围为( )
,若x,y满足不等式|x|+|y|≤1,则z的取值范围为( )| A.[﹣2,2] | B.[﹣2,3] | C.[﹣3,2] | D.[﹣3,3] |
D
∵ =(x+z,3),
=(x+z,3), =(2,y﹣z),
=(2,y﹣z),
又∵ ⊥
⊥
∴(x+z)×2+3×(y﹣z)=2x+3y﹣z=0,
即z=2x+3y
∵满足不等式|x|+|y|≤1的平面区域如下图所示:
由图可知当x=0,y=1时,z取最大值3,
当x=0,y=﹣1时,z取最小值﹣3,
故z的取值范围为[﹣3,3]
故选D

 =(x+z,3),
=(x+z,3), =(2,y﹣z),
=(2,y﹣z),又∵
 ⊥
⊥
∴(x+z)×2+3×(y﹣z)=2x+3y﹣z=0,
即z=2x+3y
∵满足不等式|x|+|y|≤1的平面区域如下图所示:
由图可知当x=0,y=1时,z取最大值3,
当x=0,y=﹣1时,z取最小值﹣3,
故z的取值范围为[﹣3,3]
故选D


练习册系列答案
相关题目
 ,则z=(x+1)2+y2的最大值为( )
,则z=(x+1)2+y2的最大值为( )
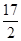
 满足线性约束条件
满足线性约束条件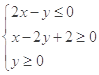 ,则
,则 的最大值为( )
的最大值为( ) 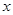 、
、 满足约束条件
满足约束条件 ,则
,则 的最小值是 .
的最小值是 .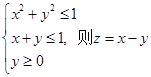 的取值范围是________.
的取值范围是________. 那么2x-y的最大值为
那么2x-y的最大值为 满足方程C:
满足方程C: ,则
,则 的最大值是___________.
的最大值是___________. ,满足
,满足 ,x≥1,则
,x≥1,则 的最大值为 .
的最大值为 . 满足约束条件
满足约束条件 则
则 的最小值为
的最小值为